题目内容
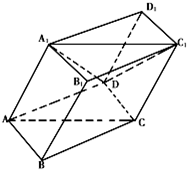如图，棱柱ABCD-A1B1C1D1的底面ABCD为菱形，平面AA1C1C⊥平面ABCD．?（1）证明：BD⊥AA1；?
（2）证明：平面AB1C∥平面DA1C1
（3）在直线CC1上是否存在点P，使BP∥平面DA1C1？若存在，求出点P的位置；若不存在，说明理由．
分析：（1）连BD，则BD⊥AC，再根据面面垂直的性质定理可得：BD⊥平面AA1C1C，进而根据线面垂直的性质定理可得：BD⊥AA1?
（2）连AB1，B1C，由棱柱ABCD-A1B1C1D1的性质知：AB1∥DC1，AD∥B1C，AB1∩B1C=B1，A1D∩DC1=D，则根据面面平行的判定定理即可证明结论．?
（3）存在这样的点P，根据平行六面体的性质可得：A1D∥B1C，在C1C的延长线上取点P，使C1C=CP，连接BP，得到BB1∥CP，即可得到BP∥A1D，进而得到线面平行．
（2）连AB1，B1C，由棱柱ABCD-A1B1C1D1的性质知：AB1∥DC1，AD∥B1C，AB1∩B1C=B1，A1D∩DC1=D，则根据面面平行的判定定理即可证明结论．?
（3）存在这样的点P，根据平行六面体的性质可得：A1D∥B1C，在C1C的延长线上取点P，使C1C=CP，连接BP，得到BB1∥CP，即可得到BP∥A1D，进而得到线面平行．
解答：证明：（1）连BD，
∵面ABCD为菱形，∴BD⊥AC
因为平面AA1C1C⊥平面ABCD，平面AA1C1C∩平面ABCD=AC，?
所以BD⊥平面AA1C1C，
又因为AA1?平面AA1C1C，
所以BD⊥AA1?
（2）连AB1，B1C，由棱柱ABCD-A1B1C1D1的性质知：AB1∥DC1，AD∥B1C，AB1∩B1C=B1，A1D∩DC1=D，
所以由面面平行的判定定理知：平面AB1C∥平面DA1C1?
（3）存在这样的点P，
因为A1B1∥AB∥DC，
所以四边形A1B1CD为平行四边形．?
所以A1D∥B1C，
在C1C的延长线上取点P，使C1C=CP，连接BP，
因为B1B∥CC1，
所以BB1∥CP，
所以四边形BB1CP为平行四边形，即BP∥B1C，
所以BP∥A1D，
所以BP∥平面DA1C1，
所以在直线CC1上是否存在点P，使BP∥平面DA1C1．
∵面ABCD为菱形，∴BD⊥AC
因为平面AA1C1C⊥平面ABCD，平面AA1C1C∩平面ABCD=AC，?
所以BD⊥平面AA1C1C，
又因为AA1?平面AA1C1C，
所以BD⊥AA1?
（2）连AB1，B1C，由棱柱ABCD-A1B1C1D1的性质知：AB1∥DC1，AD∥B1C，AB1∩B1C=B1，A1D∩DC1=D，
所以由面面平行的判定定理知：平面AB1C∥平面DA1C1?
（3）存在这样的点P，
因为A1B1∥AB∥DC，
所以四边形A1B1CD为平行四边形．?
所以A1D∥B1C，
在C1C的延长线上取点P，使C1C=CP，连接BP，
因为B1B∥CC1，
所以BB1∥CP，
所以四边形BB1CP为平行四边形，即BP∥B1C，
所以BP∥A1D，
所以BP∥平面DA1C1，
所以在直线CC1上是否存在点P，使BP∥平面DA1C1．
点评：本题主要考查线面平行、线线平行、面面平行的判定定理与性质定理，解决此类问题的关键是熟练掌握有关定理以及空间几何体中点、线、面之间的位置关系．
练习册系列答案
相关题目
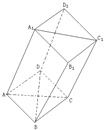如图，棱柱ABCD-A1B1C1D1的所有棱长都等于2，∠ABC和∠A1B1C1均为60°，平面AA1C1C⊥平面ABCD．
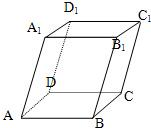如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形，侧棱与底边长均为a，且∠A1AD=∠A1AB=60°．
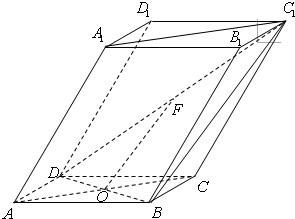17、如图，棱柱ABCD-A1B1C1D1的底面ABCD为菱形，AC∩BD=O，侧棱AA1⊥BD，点F为DC1的中点．
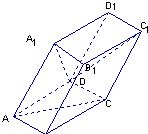如图，棱柱ABCD-A1B1C1D1的所有棱长都等于2，∠ABC=60°，平面AA1CC1⊥平面ABCD，∠A1AC=60°