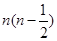题目内容
数列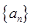 满足
满足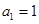 ,且对任意的正整数
,且对任意的正整数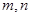 都有
都有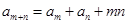 ,则
,则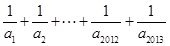 = .
= .
【答案】
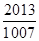
【解析】
试题分析:由于m、n是任意的正整数,结合题意,取特殊值可得答案解:由于对任意的正整数m、n,都有am+n=mn+am+an,,取n=1,代入可得am+1=mn+am+a1,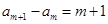 ,那么根据累加法可知,数
,那么根据累加法可知,数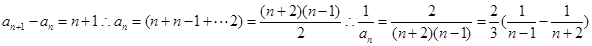 那么裂项求和可知
那么裂项求和可知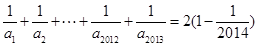 =
=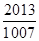 ,故答案为
,故答案为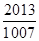 。
。
考点:数列的递推关系
点评:主要是考查了数列求和的运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
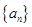 满足
满足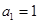 ,且对任意的正整数
,且对任意的正整数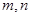 都有
都有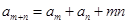 ,则
,则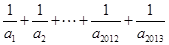 =
.
=
. 定义如下表,数列
定义如下表,数列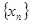 满足
满足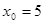 ,且对任意的自然数均有
,且对任意的自然数均有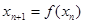 ,则
,则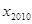 等于(
)
等于(
)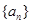 满足
满足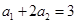 ,且对任意的
,且对任意的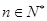 ,点
,点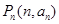 都有
都有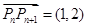 ,则
,则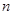 项和
项和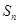 为( )
为( )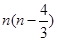 B.
B.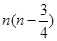 C.
C.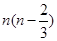 D.
D.