题目内容
已知拋物线y2=2px(p>0)上一动点P,抛物线内一点A(3,2),F为焦点且|PA|+|PF|的最小值为 .(1)求抛物线的方程以及使得|PA|+|PF|取最小值时的P点坐标;(2)过(1)中的P点作两条互相垂直的直线与抛物线分别交于C、D两点,直线CD是否过一定点?若是,求出该定点的坐标,若不是,请说明理由.
.(1)求抛物线的方程以及使得|PA|+|PF|取最小值时的P点坐标;(2)过(1)中的P点作两条互相垂直的直线与抛物线分别交于C、D两点,直线CD是否过一定点?若是,求出该定点的坐标,若不是,请说明理由.
【答案】分析:(1)由已知,(|PA|+|PF|)min=3+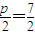 ,由此能求出抛物线方程和P点坐标.
,由此能求出抛物线方程和P点坐标.
(2)设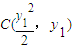 ,
,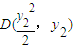 ,则直线CD的方程为
,则直线CD的方程为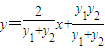 ,由PC⊥PD,得y1y2=-8-2(y1+y2),代入直线CD,得
,由PC⊥PD,得y1y2=-8-2(y1+y2),代入直线CD,得 ,由此知直线CD过定点(4,-2).
,由此知直线CD过定点(4,-2).
解答:解:(1)由已知,(|PA|+|PF|)min=3+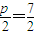 ,
,
∴p=1,
∴抛物线方程为:y2=2x,
此时P点坐标为(2,2).
(2)设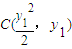 ,
,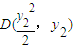 ,
,
则直线CD的方程为: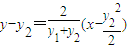 ,
,
即: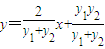 ,
,
∵PC⊥PD,∴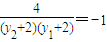 ,
,
∴y1y2=-8-2(y1+y2),
代入直线CD,得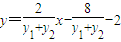 ,
,
即: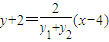 ,
,
∴直线CD过定点(4,-2).
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与抛物线的相关知识,解题时要认真审题,注意合理地进行等价转化.
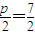 ,由此能求出抛物线方程和P点坐标.
,由此能求出抛物线方程和P点坐标.(2)设
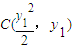 ,
,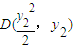 ,则直线CD的方程为
,则直线CD的方程为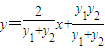 ,由PC⊥PD,得y1y2=-8-2(y1+y2),代入直线CD,得
,由PC⊥PD,得y1y2=-8-2(y1+y2),代入直线CD,得 ,由此知直线CD过定点(4,-2).
,由此知直线CD过定点(4,-2).解答:解:(1)由已知,(|PA|+|PF|)min=3+
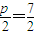 ,
,∴p=1,
∴抛物线方程为:y2=2x,
此时P点坐标为(2,2).
(2)设
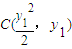 ,
,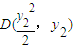 ,
,则直线CD的方程为:
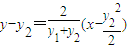 ,
,即:
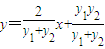 ,
,∵PC⊥PD,∴
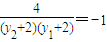 ,
,∴y1y2=-8-2(y1+y2),
代入直线CD,得
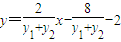 ,
,即:
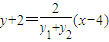 ,
,∴直线CD过定点(4,-2).
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与抛物线的相关知识,解题时要认真审题,注意合理地进行等价转化.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 .(1)求抛物线的方程以及使得|PA|+|PF|取最小值时的P点坐标;(2)过(1)中的P点作两条互相垂直的直线与抛物线分别交于C、D两点,直线CD是否过一定点?若是,求出该定点的坐标,若不是,请说明理由.
.(1)求抛物线的方程以及使得|PA|+|PF|取最小值时的P点坐标;(2)过(1)中的P点作两条互相垂直的直线与抛物线分别交于C、D两点,直线CD是否过一定点?若是,求出该定点的坐标,若不是,请说明理由. .(1)求抛物线的方程以及使得|PA|+|PF|取最小值时的P点坐标;(2)过(1)中的P点作两条互相垂直的直线与抛物线分别交于C、D两点,直线CD是否过一定点?若是,求出该定点的坐标,若不是,请说明理由.
.(1)求抛物线的方程以及使得|PA|+|PF|取最小值时的P点坐标;(2)过(1)中的P点作两条互相垂直的直线与抛物线分别交于C、D两点,直线CD是否过一定点?若是,求出该定点的坐标,若不是,请说明理由. .(1)求抛物线的方程以及使得|PA|+|PF|取最小值时的P点坐标;(2)过(1)中的P点作两条互相垂直的直线与抛物线分别交于C、D两点,直线CD是否过一定点?若是,求出该定点的坐标,若不是,请说明理由.
.(1)求抛物线的方程以及使得|PA|+|PF|取最小值时的P点坐标;(2)过(1)中的P点作两条互相垂直的直线与抛物线分别交于C、D两点,直线CD是否过一定点?若是,求出该定点的坐标,若不是,请说明理由. .(1)求抛物线的方程以及使得|PA|+|PF|取最小值时的P点坐标;(2)过(1)中的P点作两条互相垂直的直线与抛物线分别交于C、D两点,直线CD是否过一定点?若是,求出该定点的坐标,若不是,请说明理由.
.(1)求抛物线的方程以及使得|PA|+|PF|取最小值时的P点坐标;(2)过(1)中的P点作两条互相垂直的直线与抛物线分别交于C、D两点,直线CD是否过一定点?若是,求出该定点的坐标,若不是,请说明理由.