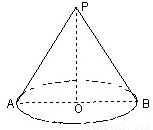
题目内容
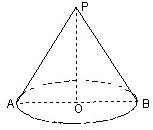 圆锥的底面圆周长为6π,高为
圆锥的底面圆周长为6π,高为 .求:
.求:
(1)圆锥的侧面积和体积;
(2)圆锥侧面展开图的扇形的圆心角的大小.
解:(1)设圆锥底面半径为R,由已知得2πR=6π,所以R=3,(3分)
又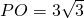 ,在Rt△POA中,得PA=6,
,在Rt△POA中,得PA=6,
即母线的长为6.(5分)
所以圆锥的侧面积为S=πR•PA=18π;(6分)
体积为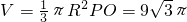 .(7分)
.(7分)
(2)圆锥侧面展开图的扇形半径就是圆锥的母线长,(8分)
扇形的弧长就是圆锥底面圆的周长,(9分)
所以圆锥侧面展开图的扇形的圆心角的弧度数为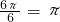 ,
,
即圆锥侧面展开图的扇形的圆心角为180°.(12分)
分析:(1)设圆锥底面半径为R,利用周长求出底面半径,求出圆锥的母线长,然后圆锥的侧面积和体积;
(2)圆锥侧面展开图的扇形半径就是圆锥的母线长,扇形的弧长就是圆锥底面圆的周长,利用扇形弧长公式,求出圆锥侧面展开图的扇形的圆心角的大小.
点评:本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.
又
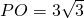 ,在Rt△POA中,得PA=6,
,在Rt△POA中,得PA=6,即母线的长为6.(5分)
所以圆锥的侧面积为S=πR•PA=18π;(6分)
体积为
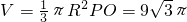 .(7分)
.(7分)(2)圆锥侧面展开图的扇形半径就是圆锥的母线长,(8分)
扇形的弧长就是圆锥底面圆的周长,(9分)
所以圆锥侧面展开图的扇形的圆心角的弧度数为
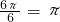 ,
,即圆锥侧面展开图的扇形的圆心角为180°.(12分)
分析:(1)设圆锥底面半径为R,利用周长求出底面半径,求出圆锥的母线长,然后圆锥的侧面积和体积;
(2)圆锥侧面展开图的扇形半径就是圆锥的母线长,扇形的弧长就是圆锥底面圆的周长,利用扇形弧长公式,求出圆锥侧面展开图的扇形的圆心角的大小.
点评:本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
相关题目
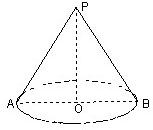 圆锥的底面圆周长为6π,高为
圆锥的底面圆周长为6π,高为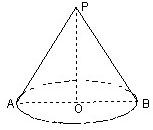
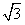 ,
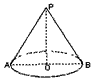
,
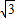 .求:
.求: