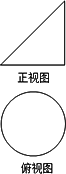
题目内容
已知某几何体是一个圆柱和一个球的组合体，球的直径和圆柱底面直径相等，它的正视图（或称主视图）如图1所示．
这个几何体的表面积是（ ）
分析：题设条件知，该组合体中，圆柱的底面半径r=1，圆柱的高为4，球半径R=1，由此能求出这个几何体的表面积．
解答：解：由题设条件知，该组合体中，
圆柱的底面半径r=1，圆柱的高为4，球半径R=1，
∴这个几何体的表面积：
S=S圆柱+S球
=2×π×12+2π×1×4+4π×12
=14π．
故选D．
圆柱的底面半径r=1，圆柱的高为4，球半径R=1，
∴这个几何体的表面积：
S=S圆柱+S球
=2×π×12+2π×1×4+4π×12
=14π．
故选D．
点评：本题考查由三视图求几何体的表面积，是基础题．解题时要认真审题，仔细解答，注意球的表面积公式的灵活运用．
练习册系列答案
相关题目
