题目内容
设
=(2cos
,2sin
),
=(sin
,
sin
),ω>0,记函数f(x)=
•
-
|
|2,且以π为最小正周期.
(Ⅰ)求ω的值;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,已知a=1,b=
,f(A)=0,求角C的值.
| a |
| ωx |
| 2 |
| ωx |
| 2 |
| b |
| ωx |
| 2 |
| 3 |
| ωx |
| 2 |
| a |
| b |
| ||
| 4 |
| a |
(Ⅰ)求ω的值;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,已知a=1,b=
| 2 |
分析:(1)由题设知f(x)=2sin
cos
+2
sin
sin
-
=2sin(ωx-
),由函数以π为最小正周期,能求出ω.
(Ⅱ)因为f(A)=0,所以sin(2A-
)=0,因为a>b,所以A=
.又因为a=1,b=
,所以由正弦定理,得sinB=
,由此能求出角C的值.
| ωx |
| 2 |
| ωx |
| 2 |
| 3 |
| ωx |
| 2 |
| ωx |
| 2 |
| 3 |
| π |
| 3 |
(Ⅱ)因为f(A)=0,所以sin(2A-
| π |
| 3 |
| π |
| 6 |
| 2 |
| ||
| 2 |
解答:解:(Ⅰ)∵
=(2cos
,2sin
),
=(sin
,
sin
),ω>0,
函数f(x)=
•
-
|
|2,
∴f(x)=2sin
cos
+2
sin
sin
-
…(1分)
=sinωx+
(1-cosωx)-
…(3分)
=2(
sinωx-
cosωx)=2sin(ωx-
).…(5分)
由T=
=π,解得ω=2.…(6分)
(Ⅱ)因为f(A)=0,所以sin(2A-
)=0,
因为在△ABC中,∵a>b,∴A>B,所以A=
.…(7分)
又因为a=1,b=
,所以由正弦定理,得
=
,
也就是sinB=
=
×
=
,
因为b>a,所以B=
或B=
.…(10分)
当B=
时,C=π-
-
=
;
当B=
时,C=π-
-
=
.…(12分)
| a |
| ωx |
| 2 |
| ωx |
| 2 |
| b |
| ωx |
| 2 |
| 3 |
| ωx |
| 2 |
函数f(x)=
| a |
| b |
| ||
| 4 |
| a |
∴f(x)=2sin
| ωx |
| 2 |
| ωx |
| 2 |
| 3 |
| ωx |
| 2 |
| ωx |
| 2 |
| 3 |
=sinωx+
| 3 |
| 3 |
=2(
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
由T=
| 2π |
| ω |
(Ⅱ)因为f(A)=0,所以sin(2A-
| π |
| 3 |
因为在△ABC中,∵a>b,∴A>B,所以A=
| π |
| 6 |
又因为a=1,b=
| 2 |
| a |
| sinA |
| b |
| sinB |
也就是sinB=
| bsinA |
| a |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
因为b>a,所以B=
| π |
| 4 |
| 3π |
| 4 |
当B=
| π |
| 4 |
| π |
| 6 |
| π |
| 4 |
| 7π |
| 12 |
当B=
| 3π |
| 4 |
| π |
| 6 |
| 3π |
| 4 |
| π |
| 12 |
点评:本题考查正弦定理的应用,解题时要认真审题,注意向量知识、三角函数恒等变换、三角形内角和定理等知识点的合理运用.

练习册系列答案
相关题目
已知向量
=(2cosωx,1),
=(sinωx+cosωx,-1),(ω∈R,ω>0),设函数f(x)=
•
(x∈R),若f(x)的最小正周期为
.
(1)求ω的值;
(2)求f(x)的单调区间.
| a |
| b |
| a |
| b |
| π |
| 2 |
(1)求ω的值;
(2)求f(x)的单调区间.
 =(2cosωx,
=(2cosωx, sinωx),
sinωx), =(cosωx,2cosωx)(w>0),函数f(x)=
=(cosωx,2cosωx)(w>0),函数f(x)= ,求
,求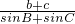 的值.
的值.