Question

设M是又满足下列性质的函数f（x）构成的集合：在定义域存中在x，使得f（x+1）=f（x）+f（1）成立已知下列函数：
①f（x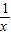）=；②f（x）=2^x；③f（x）=lg（x²+2）；④f（x）=cosπx，其中属于集合M的函数是（ ）
A．①③
B．②③
C．③④
D．②④

Answer 1

【答案】分析：根据集合M的定义，可根据函数的解析式，f（x+1）=f（x）+f（1）构造方程，若方程有根，说明函数符合集合M的定义，若方程无根，说明函数不符号集合M的定义，由此对四个函数逐一进行判断，即可得到答案．
解答：解：①中，若存在x，使f（x+1）=f（x）+f（1）
则，即x²+x+1=0，
∵△=1-4=-3＜0，故方程无解．即f（x）=∉M
②中，存在x=1，使f（x+1）=2^x+1=f（x）+f（1）=2^x+2成立，即f（x）=2^x∈M；
③中，若存在x，使f（x+1）=f（x）+f（1）
则lg[（x+1）²+2]=lg（x²+2）+lg3
即2x²-2x+3=0，
∵△=4-24=-20＜0，故方程无解．即f（x）=lg（x²+2）∉M
④存在x=，使f（x+1）=cosπ（x+1）=f（x）+f（1）=cosπx+cosπ成立，即f（x）=cosπx∈M；
综上可知②④中的函数属于集合M，
故选D
点评：本题考查的知识点是元素与集合关系的判断，及其它方程的解法，掌握判断元素与集合关系的方法，即元素是否满足集合的性质是解答本题的关键．