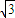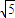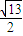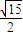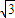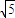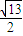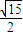题目内容
已知实数a满足方程:(x-a+1)2+(y-1)2=1,当0≤y≤b(b∈R)时,由此方程可以确定一个偶函数y=f(x),则抛物线y2=-4x的焦点到动点(a,b)所构成轨迹上点的距离的最大值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:由题可知当0≤y≤b(b∈R)时,由此方程可以确定一个偶函数y=f(x)即x-a+1=-x-a+1得到x=0求出a的最大值,或x-a+1=x+a-1得到a=1;同时根据方程得到b的最大值为2;抛物线y2=-4x的焦点为(-1.,0),利用两点间的距离公式求出距离,找出最大值即可.
解答:解:因为当0≤y≤b(b∈R)时,由此方程可以确定一个偶函数y=f(x)
则(x-a+1)2=(-x-a+1)2解得x=0或a=1;当a=1时方程变为:x2+(y-1)2=1舍去;当x=0时得到(a-1)2+(y-1)2=1
即可求得b的最大值为2,a的最大值为0,
抛物线的焦点坐标为(-1,0)则两点的距离d=
=
故选B
则(x-a+1)2=(-x-a+1)2解得x=0或a=1;当a=1时方程变为:x2+(y-1)2=1舍去;当x=0时得到(a-1)2+(y-1)2=1
即可求得b的最大值为2,a的最大值为0,
抛物线的焦点坐标为(-1,0)则两点的距离d=
| (a+1)2+b2 |
| 5 |
故选B
点评:考查学生综合运用函数与方程的能力,会利用抛物线简单性质的能力,会求两点间的距离.

练习册系列答案
相关题目