题目内容
已知函数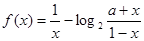 为奇函数.
为奇函数.
(1)求常数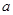 的值;
的值;
(2)判断函数的单调性,并说明理由;
(3)函数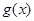 的图象由函数
的图象由函数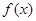 的图象先向右平移2个单位,再向上平移2个单位得到,写出
的图象先向右平移2个单位,再向上平移2个单位得到,写出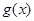 的一个对称中心,若
的一个对称中心,若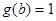 ,求
,求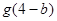 的值.
的值.
【答案】
(1)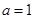 ;(2)减函数,证明见解析;(3)对称中心
;(2)减函数,证明见解析;(3)对称中心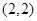 ,
, .
.
【解析】
试题分析:(1)本题唯一的条件是 为奇函数,故其定义域关于原点对称,通过求函数的定义域可求得
为奇函数,故其定义域关于原点对称,通过求函数的定义域可求得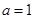 ,当然这时还要根据奇函数的定义验证
,当然这时还要根据奇函数的定义验证 确实是奇函数;(2)要判断函数的单调性,可根据复合函数单调性的性质确定,然后再根据定义证明,而函数
确实是奇函数;(2)要判断函数的单调性,可根据复合函数单调性的性质确定,然后再根据定义证明,而函数 为奇函数,故只要判断函数在区间
为奇函数,故只要判断函数在区间 上的单调性即可,变形
上的单调性即可,变形 为
为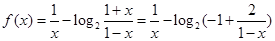 可得
可得 在
在 是递减,当然它在
是递减,当然它在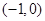 上也是递减的,然后用单调性定义田加以证明;(3)
上也是递减的,然后用单调性定义田加以证明;(3) 为奇函数,它的对称中心为
为奇函数,它的对称中心为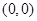 ,
,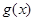 的图象是由
的图象是由 的图象平移过去的,因此对称中心也相应平移,即
的图象平移过去的,因此对称中心也相应平移,即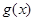 对称中心为
对称中心为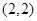 ,函数
,函数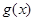 的图象对称中心为
的图象对称中心为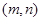 ,则
,则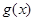 有性质:
有性质: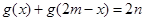 ,因此本题是有
,因此本题是有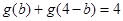 ,即
,即 .
.
试题解析:(1)因为函数为奇函数,所以定义域关于原点对称,由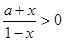 ,得
,得
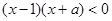 ,所以
,所以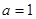 .
2分
.
2分
这时 满足
满足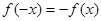 ,函数为奇函数,因此
,函数为奇函数,因此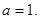 4分
4分
(2)函数为单调递减函数.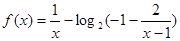
法一:用单调性定义证明;
法二:利用已有函数的单调性加以说明.
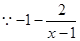 在
在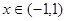 上单调递增,因此
上单调递增,因此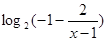 单调递增,又
单调递增,又 在
在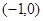 及
及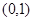 上单调递减,因此函数
上单调递减,因此函数 在
在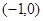 及
及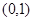 上单调递减;
上单调递减;
法三:函数定义域为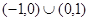 ,说明函数在
,说明函数在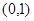 上单调递减,因为函数为奇函数,因此函数在
上单调递减,因为函数为奇函数,因此函数在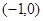 上也是单调递减,因此函数
上也是单调递减,因此函数 在
在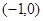 及
及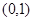 上单调递减.
上单调递减.
10分
(本题根据具体情况对照给分)
(3)因为函数 为奇函数,因此其图像关于坐标原点(0,0)对称,根据条件得到函数
为奇函数,因此其图像关于坐标原点(0,0)对称,根据条件得到函数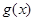 的一个对称中心为
的一个对称中心为 ,
13分
,
13分
因此有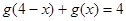 ,因为
,因为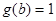 ,因此
,因此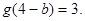 16分
16分
考点:(1)奇函数的性质;(2)函数的单调性;(3)函数图象的平移,函数图象的对称性.

练习册系列答案
相关题目
 为奇函数,
为奇函数, 为偶函数,且
为偶函数,且 .
. ,则称
,则称 是函数
是函数 为奇函数,
为奇函数, 为偶函数
为偶函数 ,且
,且 .
. ,则称
,则称 是函数
是函数