题目内容
定义在区间[-1,1]上的奇函数f(x)满足:对任意a,b∈[-1,1],a+b≠0,都有
<0,f(1)=-3.
(1)证明:f(x)在[-1,1]上是减函数;
(2)解不等式:f(x+1)+f(x2-1)>0;
(3)若不等式f(x)≤m2+2am对任意x,a∈[-1,1]恒成立,求实数m的取值范围.
| f(a)+f(b) | a+b |
(1)证明:f(x)在[-1,1]上是减函数;
(2)解不等式:f(x+1)+f(x2-1)>0;
(3)若不等式f(x)≤m2+2am对任意x,a∈[-1,1]恒成立,求实数m的取值范围.
分析:(1)依题意,可求得a,b∈[-1,1]时,
<0,从而可证f(x)在[-1,1]上是减函数;
(2)利用f(x)在[-1,1]上是减函数,解不等式组-1≤x2-1<-x-1≤1即可求得其解集;
(3)依题意知,m2+2am≥3,a∈[-1,1]恒成立,构造函数g(a)=2ma+m2,a∈[-1,1],由
即可求得实数m的取值范围.
| f(a)-f(b) |
| a-b |
(2)利用f(x)在[-1,1]上是减函数,解不等式组-1≤x2-1<-x-1≤1即可求得其解集;
(3)依题意知,m2+2am≥3,a∈[-1,1]恒成立,构造函数g(a)=2ma+m2,a∈[-1,1],由
|
解答:证明:(1)∵函数f(x)是区间[-1,1]上的奇函数,
∴f(a)-f(b)=f(a)+f(-b),
∵对任意a,b∈[-1,1],a+b≠0,都有
<0,
∴当a,b∈[-1,1],
=
<0,
即奇函数f(x)曲线上任意两点(a,f(a))与(b,f(b))的斜率为负值,
∴f(x)在[-1,1]上是减函数;
(2)由f(x+1)+f(x2-1)>0得:f(x2-1)>-f(x+1)=f(-x-1),
∵f(x)在[-1,1]上是减函数,
∴-1≤x2-1<-x-1≤1,
解得:-1<x<0,
∴不等式:f(x+1)+f(x2-1)>0的解集为(-1,0).
(3)∵不等式f(x)≤m2+2am对任意x,a∈[-1,1]恒成立,
∴m2+2am≥f(x)max(-1≤x≤1)恒成立,
又f(x)在[-1,1]上是减函数,f(1)=-3,
∴当x∈[-1,1]时,f(x)max=f(-1)=-f(1)=3,
∴m2+2am≥3,a∈[-1,1]恒成立,
令g(a)=2ma+m2,a∈[-1,1],
依题意,
,即
,
解得:m≤-3或m≥3,
∴实数m的取值范围是:(-∞,-3]∪[3,+∞).
∴f(a)-f(b)=f(a)+f(-b),
∵对任意a,b∈[-1,1],a+b≠0,都有
| f(a)+f(b) |
| a+b |
∴当a,b∈[-1,1],
| f(a)+f(-b) |
| a+(-b) |
| f(a)-f(b) |
| a-b |
即奇函数f(x)曲线上任意两点(a,f(a))与(b,f(b))的斜率为负值,
∴f(x)在[-1,1]上是减函数;
(2)由f(x+1)+f(x2-1)>0得:f(x2-1)>-f(x+1)=f(-x-1),
∵f(x)在[-1,1]上是减函数,
∴-1≤x2-1<-x-1≤1,
解得:-1<x<0,
∴不等式:f(x+1)+f(x2-1)>0的解集为(-1,0).
(3)∵不等式f(x)≤m2+2am对任意x,a∈[-1,1]恒成立,
∴m2+2am≥f(x)max(-1≤x≤1)恒成立,
又f(x)在[-1,1]上是减函数,f(1)=-3,
∴当x∈[-1,1]时,f(x)max=f(-1)=-f(1)=3,
∴m2+2am≥3,a∈[-1,1]恒成立,
令g(a)=2ma+m2,a∈[-1,1],
依题意,
|
|
解得:m≤-3或m≥3,
∴实数m的取值范围是:(-∞,-3]∪[3,+∞).
点评:本题考查抽象函数及其应用,着重考查函数单调性,考查方程思想、化归思想、构造函数思想的综合运用,属于难题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
 为奇函数..
为奇函数..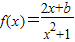 为奇函数..
为奇函数.. 为奇函数..
为奇函数..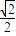 时,f (x)取得极大值
时,f (x)取得极大值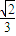 ,并且函数y=f(x)的图象关于y轴对称.
,并且函数y=f(x)的图象关于y轴对称.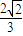 (x∈R).
(x∈R).