题目内容
设A,B,C,D是空间四个不同的点,在下列命题中,不正确的是( )A.若AC与BD共面,则AD与BC共面
B.若AC与BD是异面直线,则AD与BC是异面直线
C.若AB=AC,DB=DC,则AD=BC
D.若AB=AC,DB=DC,则AD⊥BC
解析:A.若AC与BD共面,则A、B、C、D四点共面.
∴AD与BC共面,故A正确.
B.假设AD与BC共面,则A、B、C、D四点共面.
∴AC与BD也共面,此结论与AD与BD是异面直线矛盾.
∴假设不成立,即AD与BC是异面直线.
C.如下图两个有公共底边BC的等腰三角形△ABC,△DBC.
AD的值随开口大小而变化而BC不变,这就说明AD≠BC故C不正确.
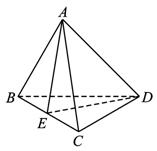
D.若A、B、C、D四点共面命题显然成立,若这四点不共面如右图,取BC中点E、连结AE、DE.
∵AB=AC,DB=DC,∴AE⊥BC,DE⊥BC.∵AE∩DE=E,AE![]() 平面ADE,DE
平面ADE,DE![]() 平面ADE,
平面ADE,
∴BC⊥平面ADE.∵AD![]() 平面ADE,∴BC⊥AD.
平面ADE,∴BC⊥AD.
答案:C

练习册系列答案
相关题目
 ,则有( )
,则有( ) B、
B、
 D、
D、
 是两个非空实数集合,定义集合
是两个非空实数集合,定义集合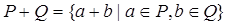 .
. ,则
,则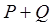 中元素的个数是( )
中元素的个数是( )