题目内容
设函数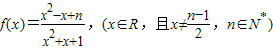
的最小值为an，最大值为bn，记cn=（1-an）（1-bn），则数列{cn}为（ ）A．是常数列
B．是公比不为1的等比数列
C．是公差不为0的等差数列
D．不是等差数列也不是等比数列
【答案】分析：先利用判别式法求出函数的值域，从而求出an与bn，代入cn=（1-an）（1-bn），然后判定数列{cn}的规律．
解答：解：令y=f（x）=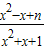
（x∈R，x≠
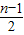，x∈N*），
则y（x2+x+1）=x2-x+n，
整理得：（y-1）x2+（y+1）x+y-n=0，
△=（y+1）2-4（y-1）（y-n）≥0，
解得：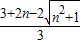
≤y≤
．
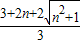∴f（x）的最小值为an=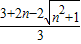
，
最大值为bn=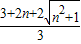
，
∴cn=（1-an）（1-bn）=-
．
∴数列{cn}是常数数列
故选A．
点评：本题主要考查了分式函数的值域，以及数列的判定，同时考查了计算能力，属于中档题．
解答：解：令y=f（x）=
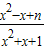（x∈R，x≠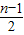，x∈N*），则y（x2+x+1）=x2-x+n，
整理得：（y-1）x2+（y+1）x+y-n=0，
△=（y+1）2-4（y-1）（y-n）≥0，
解得：
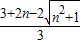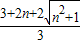≤y≤．∴f（x）的最小值为an=
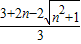，最大值为bn=
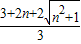，∴cn=（1-an）（1-bn）=-
．∴数列{cn}是常数数列
故选A．
点评：本题主要考查了分式函数的值域，以及数列的判定，同时考查了计算能力，属于中档题．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目