题目内容
下列命题中是假命题的是（ ）
| A、存在α，β∈R，tan（α+β）=tanα+tanβ | B、对任意x＞0，lg2x+lgx+1＞0 | C、△ABC中，A＞B的充要条件是sinA＞sinB | D、对任意φ∈R，y=sin（2x+φ）都不是偶函数 |
分析：对于A，α=β=0时成立；对于B，由于判别式小于0，故正确；对于C，利用正弦定理可知正确；对于D，∅=
，函数即为偶函数，故可得结论．
| π |
| 2 |
解答：解：对于A，α=β=0时成立；对于B，由于判别式小于0，故正确；对于C，利用正弦定理可知正确；对于D，∅=
，函数即为偶函数，故选D．
| π |
| 2 |
点评：本题主要考查命题真假的判断，真命题需要有充分的利用，而假命题列举反例即可．
练习册系列答案
阅读快车系列答案
相关题目
关于
的方程
，下列四个命题中是假命题的是 （ ）
，使得方程恰有2个不同的实根；
”是“直线(m+2)x+3my+1=0与直线(m－2)x+(m+2)y－3=0垂直”的充要条件
“是“
的夹角为锐角”的充要条件
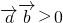”是“直线（m+2）x+3my+1=0与直线（m-2）x+（m+2）y-3=0垂直”的充要条件