题目内容
 如图①边长为1的正方形ABCD中,点E、F分别为AB、BC的中点,将△BEF剪去,将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点P得一三棱锥如图②示.
如图①边长为1的正方形ABCD中,点E、F分别为AB、BC的中点,将△BEF剪去,将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点P得一三棱锥如图②示.
(1)求证:PD⊥EF;
(2)求三棱锥P-DEF的体积;
(3)求点E到平面PDF的距离.
(1)证明:依题意知图1折前AD⊥AE,CD⊥CF,-------------------------------(1分)
∴PD⊥PE,PF⊥PD,-------------------------------------------------------(2分)
∵PE∩PF=P,∴PD⊥平面PEF-----------------------------------(4分)
又∵EF?平面PEF,∴PD⊥EF----------------------------------------(5分)
(2)解法1:依题意知图1中AE=CF= ,∴PE=PF=
,∴PE=PF= ,
,
在△BEF中, ,-----(6分)
,-----(6分)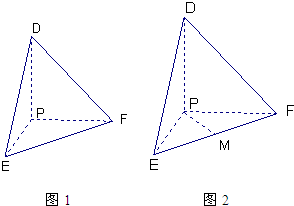
在△PEF中,PE2+PF2=EF2,
∴ ------(8分)
------(8分)
∴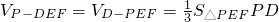 =
= .-----(10分)
.-----(10分)
解法2:依题意知图2中AE=CF= ,∴PE=PF=
,∴PE=PF= ,
,
在△BEF中 ,------------------(6分)
,------------------(6分)
取EF的中点M,连接PM
则PM⊥EF,∴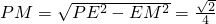 ---------(7分)
---------(7分)
∴ ---------------(8分)
---------------(8分)
∴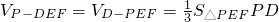 =
= .------------------------------(10分)
.------------------------------(10分)
(3)由(2)知PE⊥PF,又PE⊥PD,∴PE⊥平面PDF---------------------(12分)
∴线段PE的长就是点E到平面PDF的距离--------------------------------------(13分)
∵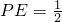 ,∴点E到平面PDF的距离为
,∴点E到平面PDF的距离为 .-------------------------------------(14分)
.-------------------------------------(14分)
分析:(1)证明PD⊥EF,只需证明PD⊥平面PEF即可;
(2)解法1:依题意知图1中AE=CF= ,从而PE=PF=
,从而PE=PF= ,证明PE⊥PF,利用
,证明PE⊥PF,利用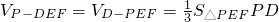 可求;
可求;
解法2:依题意知图2中AE=CF= ,从而PE=PF=
,从而PE=PF= ,取EF的中点M,连接PM,则PM⊥EF,利用
,取EF的中点M,连接PM,则PM⊥EF,利用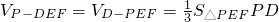 可求;
可求;
(3)由(2)知PE⊥平面PDF,从而线段PE的长就是点E到平面PDF的距离.
点评:本题考查线线垂直,考查三棱锥的体积,考查点面距离的计算,解题的关键是利用线面垂直证明线线垂直,掌握转换底面求体积.
∴PD⊥PE,PF⊥PD,-------------------------------------------------------(2分)
∵PE∩PF=P,∴PD⊥平面PEF-----------------------------------(4分)
又∵EF?平面PEF,∴PD⊥EF----------------------------------------(5分)
(2)解法1:依题意知图1中AE=CF=
 ,∴PE=PF=
,∴PE=PF= ,
,在△BEF中,
 ,-----(6分)
,-----(6分)
在△PEF中,PE2+PF2=EF2,
∴
 ------(8分)
------(8分)∴
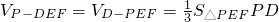 =
= .-----(10分)
.-----(10分)解法2:依题意知图2中AE=CF=
 ,∴PE=PF=
,∴PE=PF= ,
,在△BEF中
 ,------------------(6分)
,------------------(6分)取EF的中点M,连接PM
则PM⊥EF,∴
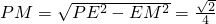 ---------(7分)
---------(7分)∴
 ---------------(8分)
---------------(8分)∴
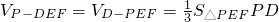 =
= .------------------------------(10分)
.------------------------------(10分)(3)由(2)知PE⊥PF,又PE⊥PD,∴PE⊥平面PDF---------------------(12分)
∴线段PE的长就是点E到平面PDF的距离--------------------------------------(13分)
∵
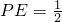 ,∴点E到平面PDF的距离为
,∴点E到平面PDF的距离为 .-------------------------------------(14分)
.-------------------------------------(14分)分析:(1)证明PD⊥EF,只需证明PD⊥平面PEF即可;
(2)解法1:依题意知图1中AE=CF=
 ,从而PE=PF=
,从而PE=PF= ,证明PE⊥PF,利用
,证明PE⊥PF,利用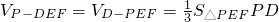 可求;
可求;解法2:依题意知图2中AE=CF=
 ,从而PE=PF=
,从而PE=PF= ,取EF的中点M,连接PM,则PM⊥EF,利用
,取EF的中点M,连接PM,则PM⊥EF,利用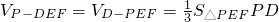 可求;
可求;(3)由(2)知PE⊥平面PDF,从而线段PE的长就是点E到平面PDF的距离.
点评:本题考查线线垂直,考查三棱锥的体积,考查点面距离的计算,解题的关键是利用线面垂直证明线线垂直,掌握转换底面求体积.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
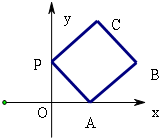 (北京卷理14)如图放置的边长为1的正方形PABC沿x轴滚动.设顶点p(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为
(北京卷理14)如图放置的边长为1的正方形PABC沿x轴滚动.设顶点p(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为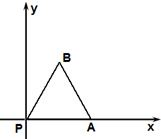 如图放置的边长为1的正三角形PAB沿x轴滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系式是y=f(x),则f(x)在区间[-2,1]上的解析式是
如图放置的边长为1的正三角形PAB沿x轴滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系式是y=f(x),则f(x)在区间[-2,1]上的解析式是 如图放置的边长为1的正方形PABC沿x轴滚动.设顶点p(x,y)的轨迹方程是y=f(x),设f(x)的最小正周期为T,y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为S,则ST=
如图放置的边长为1的正方形PABC沿x轴滚动.设顶点p(x,y)的轨迹方程是y=f(x),设f(x)的最小正周期为T,y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为S,则ST= (2011•洛阳一模)如图放置的边长为1的正三角形ABC沿x轴的正方向滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系是y=f(x).则f(x)在两个相邻零点间的图象与x轴围成的面积是
(2011•洛阳一模)如图放置的边长为1的正三角形ABC沿x轴的正方向滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系是y=f(x).则f(x)在两个相邻零点间的图象与x轴围成的面积是