题目内容
在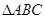 中,
中,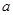 、
、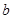 、
、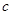 分别为角
分别为角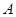 、
、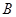 、
、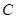 所对的边,角C是锐角,且
所对的边,角C是锐角,且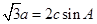 。
。
(1)求角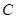 的值;
的值;
(2)若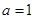 ,
,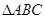 的面积为
的面积为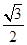 ,求
,求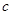 的值。
的值。
【答案】
(1) 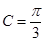 (2)
(2)
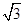
【解析】
试题分析:(1)解三角形问题, 由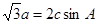 根据正弦定理可得到角C的正弦值,再根据三角形的内角和为
根据正弦定理可得到角C的正弦值,再根据三角形的内角和为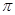 ,可得C的值.
,可得C的值.
(2)在(1)中已经知道C的值,利用面积公式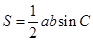 得到
得到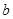 的值,再利用余弦定理解得
的值,再利用余弦定理解得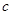 的值.
的值.
试题解析:(1)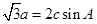 ,据正弦定理,得
,据正弦定理,得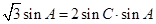 3分
3分
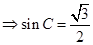 ,
因为C是锐角,所以
,
因为C是锐角,所以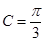 6分
6分
(2)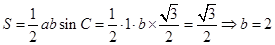 .8分
.8分
由余弦定理,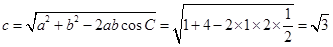 ,
,
即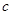 的值为
的值为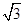 。
12分
。
12分
考点:解三角形问题,正弦定理余弦定理的应用,三角形面积公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
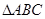 中,
中,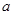 、
、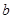 、
、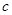 分别为角
分别为角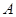 、
、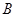 、
、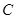 的对边
的对边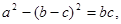
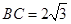 ,内角
,内角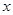 ,周长为
,周长为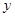 ,求
,求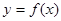 的最大值
的最大值 中,
中, 、
、 、
、 分别为角A、B、C的对边,且
分别为角A、B、C的对边,且 ,
, ,(其中
,(其中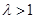 ).
). 时,求
时,求 的值;
的值; 时,求边长
时,求边长