题目内容
在一次食品卫生大检查中,执法人员从抽样中得知,目前投放我市的甲、乙两种食品的合格率分别为90%和80%.(1)今有三位同学聚会,若每人分别从两种食品中任意各取一件,求恰好有一人取到两件都是不合格品的概率.
(2)若某消费者从两种食品中任意各购一件,设ξ表示购得不合格食品的件数,试求其数学期望.
【答案】分析:首先分析题目可把三人分别从中各取一件,恰好有一人取到两件都是不合格品的事件,可看做三次独立重复试验问题.即可求得结果.然后求消费者从两种食品中任意各购一件不合格食品的件数的分布,然后由期望公式求得结果.
解答:解:(1)P(ξ=2)=0.1×0.2=0.02
因为每人从两种食品中各取一件,两件恰好都是不合格食品的概率为0.02,所以三人分别从中各取一件,恰好有一人取到两件都是不合格品的事件,可看做三次独立重复试验问题.
所以P=C31(1-0.02)2×0.02≈0.0576
(2)因为ξ=0,1,2,
则有 P(ξ=0)=0.9×0.8=0.72
P(ξ=1)=(1-0.9)×0.8+0.9×(1-0.8)=0.26
P(ξ=2)=1-0.72-0.26=0.02
所以期望Eξ=0×0.72+1×0.26+2×0.02=0.30
所以答案问哦0.30
点评:此题主要考查离散型随机变量的期望及方差的计算,属于数学在实际问题中的应用,考查同学们的分析能力.属于中档题目.
解答:解:(1)P(ξ=2)=0.1×0.2=0.02
因为每人从两种食品中各取一件,两件恰好都是不合格食品的概率为0.02,所以三人分别从中各取一件,恰好有一人取到两件都是不合格品的事件,可看做三次独立重复试验问题.
所以P=C31(1-0.02)2×0.02≈0.0576
(2)因为ξ=0,1,2,
则有 P(ξ=0)=0.9×0.8=0.72
P(ξ=1)=(1-0.9)×0.8+0.9×(1-0.8)=0.26
P(ξ=2)=1-0.72-0.26=0.02
所以期望Eξ=0×0.72+1×0.26+2×0.02=0.30
所以答案问哦0.30
点评:此题主要考查离散型随机变量的期望及方差的计算,属于数学在实际问题中的应用,考查同学们的分析能力.属于中档题目.

练习册系列答案
相关题目
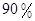 和
和 .
.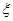 表示购得不合格食品的件数,试写出
表示购得不合格食品的件数,试写出