题目内容
在平面直角坐标系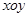 中,曲线
中,曲线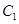 的参数方程为
的参数方程为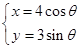 (
(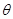 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系,得曲线
轴的非负半轴为极轴建立极坐标系,得曲线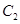 的极坐标方程为
的极坐标方程为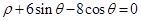 (
(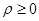 )
)
(Ⅰ)求曲线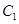 的普通方程和曲线
的普通方程和曲线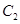 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线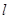 :
: 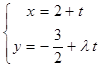 (
(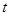 为参数)过曲线
为参数)过曲线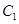 与
与 轴负半轴的交点,求与直线
轴负半轴的交点,求与直线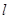 平行且与曲线
平行且与曲线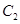 相切的直线方程
相切的直线方程
(Ⅰ) 、
、 ;(Ⅱ)
;(Ⅱ) 或
或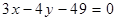
解析试题分析:(Ⅰ) 利用参数方程化普通方程、极坐标方程化直角坐标方程来求;(Ⅱ)利用点到直线的距离来求
试题解析:(Ⅰ)曲线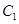 的普通方程为:
的普通方程为: ; 2分
; 2分
由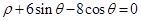 得
得 ,
,
∴曲线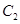 的直角坐标方程为:
的直角坐标方程为: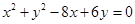 4分
4分
(或:曲线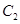 的直角坐标方程为:
的直角坐标方程为: )
)
(Ⅱ)曲线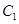 :
: 与
与 轴负半轴的交点坐标为
轴负半轴的交点坐标为 ,
,
又直线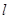 的参数方程为:
的参数方程为: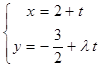 ,∴
,∴ ,得
,得 ,
,
即直线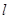 的参数方程为:
的参数方程为: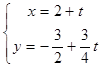
得直线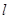 的普通方程为:
的普通方程为: , 6分
, 6分
设与直线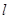 平行且与曲线
平行且与曲线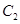 相切的直线方程为:
相切的直线方程为: 7分
7分
∵曲线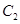 是圆心为
是圆心为 ,半径为
,半径为 的圆,
的圆,
得 ,解得
,解得 或
或 9分
9分
故所求切线方程为: 或
或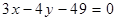 10分
10分
考点:参数方程化普通方程、极坐标方程转化为直角坐标方程,考查学生分析问题、解决问题的能力

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
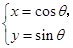 (
(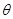 为参数),曲线C2:
为参数),曲线C2: (t为参数).
(t为参数).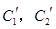 .写出
.写出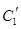 与
与 公共点的个数和C
公共点的个数和C 公共点的个数是否相同?说明你的理由.
公共点的个数是否相同?说明你的理由.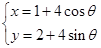 (
( 为参数),直线
为参数),直线 经过定点P(3,5),倾斜角为
经过定点P(3,5),倾斜角为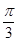 (1)写出直线
(1)写出直线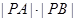 的值
的值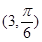 ,半径r=1.
,半径r=1.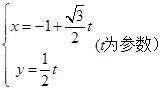 与圆交于
与圆交于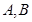 两点,求弦
两点,求弦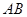 的长.
的长. (θ为参数),直线l经过定点P(2,3),倾斜角为
(θ为参数),直线l经过定点P(2,3),倾斜角为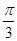 .
.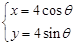 (
(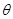 为参数),直线l经过点P(2,2),倾斜角
为参数),直线l经过点P(2,2),倾斜角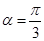 。(1)写出圆的标准方程和直线l的参数方程;
。(1)写出圆的标准方程和直线l的参数方程;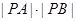 的值。
的值。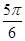 .
.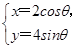 (θ为参数)交于A,B两点,求|PA|·|PB|.
(θ为参数)交于A,B两点,求|PA|·|PB|. 中,曲线
中,曲线 的参数方程为
的参数方程为 ,
, 为极点,
为极点, 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
. 时,曲线
时,曲线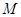 、
、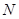 两点,求以线段
两点,求以线段 为直径的圆的直角坐标方程.
为直径的圆的直角坐标方程.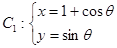
 为参数
为参数 ,在曲线
,在曲线 上求一点
上求一点 ,使它到直线
,使它到直线
 为参数
为参数