题目内容
已知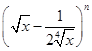 的展开式中的二项式系数之和为256.
的展开式中的二项式系数之和为256.
(Ⅰ)证明展开式中没有常数项;
(Ⅱ)求展开式中所有有理项.
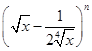 的展开式中的二项式系数之和为256.
的展开式中的二项式系数之和为256.(Ⅰ)证明展开式中没有常数项;
(Ⅱ)求展开式中所有有理项.
(Ⅰ)展开式中没有常数项.(Ⅱ .
.
 .
.本试题主要是考查了二项式定理的通项公式的运用。
(1)首先根据展开式中的二项式系数之和为256,确定出 ,n的值,然后借助通项公式得到表达式,只需要令x的幂指数为零即可,来说明是否存在。
,n的值,然后借助通项公式得到表达式,只需要令x的幂指数为零即可,来说明是否存在。
(2)而展开式中的有理项指的是让x的幂指数为整数的情况即可
解: (Ⅰ)依题意得:

 令
令 得
得

 展开式中没有常数项.
展开式中没有常数项.
(Ⅱ)当 时,
时, 为有理项.
为有理项. 展开式中所有有理项为:
展开式中所有有理项为:
(1)首先根据展开式中的二项式系数之和为256,确定出
 ,n的值,然后借助通项公式得到表达式,只需要令x的幂指数为零即可,来说明是否存在。
,n的值,然后借助通项公式得到表达式,只需要令x的幂指数为零即可,来说明是否存在。(2)而展开式中的有理项指的是让x的幂指数为整数的情况即可
解: (Ⅰ)依题意得:


 令
令 得
得

 展开式中没有常数项.
展开式中没有常数项.(Ⅱ)当
 时,
时, 为有理项.
为有理项. 展开式中所有有理项为:
展开式中所有有理项为:

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 为正整数,若
为正整数,若 和
和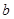 除以
除以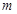 的余数相同,则称
的余数相同,则称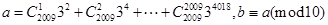 ,则
,则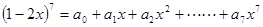 那么
那么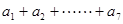 = _____.
= _____.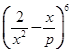 的展开式中,不含x的项是
的展开式中,不含x的项是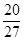 ,那么的p值为
,那么的p值为 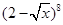 展开式中所有项的系数和为( )
展开式中所有项的系数和为( )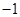
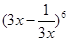 的展开式的常数项是 .(用数字作答)
的展开式的常数项是 .(用数字作答)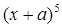 的展开式中
的展开式中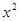 的系数为80,则a= .
的系数为80,则a= .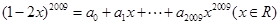 ,则
,则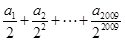 的值为 .
的值为 . 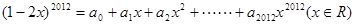 ,则
,则 .
.