题目内容
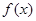 与
与 是定义在R上的两个可导函数,若
是定义在R上的两个可导函数,若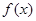 ,
, 满足
满足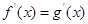 ,则
,则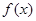 与
与 满足( )
满足( )
A.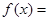  | B.  为常数函数 为常数函数 |
C.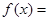 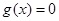 | D.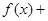  为常数函数 为常数函数 |
B
解析

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
曲线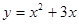 在点A(2,10)处的切线的斜率是
在点A(2,10)处的切线的斜率是
| A.4 | B.5 | C.6 | D.7 |
函数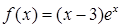 的单调增区间是
的单调增区间是
A.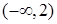 | B.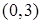 | C.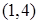 | D.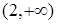 |
对于R上可导的任意函数f(x),若满足(x+1)f′(x)≥0,则有( )
| A.f(0)+f(-2)<2f(-1) | B.f(0)+f(-2)≤2f(-1) |
| C.f(0)+f(-2)>2f(-1) | D.f(0)+f(-2)≥2f(-1) |
设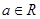 ,函数
,函数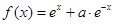 的导函数是
的导函数是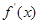 ,且
,且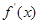 是奇函数。若曲线
是奇函数。若曲线 的一条切线的斜率是
的一条切线的斜率是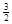 ,则切点的横坐标为( )
,则切点的横坐标为( )
A.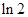 | B.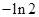 | C.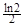 | D.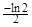 |
若 上是增函数,则实数
上是增函数,则实数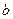 的取值范围是
的取值范围是
A.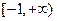 | B.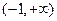 | C.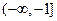 | D.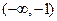 |
已知函数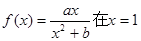 处取得极值2,则当
处取得极值2,则当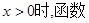

| A.有最小值2 | B.有最大值2 | C.有最小值4 | D.有最大值4 |
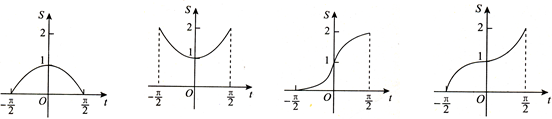
 的图象上有一点
的图象上有一点 ,此函数图象与
,此函数图象与 轴及直线
轴及直线 围成图形(如图阴影部分)的面积为
围成图形(如图阴影部分)的面积为 ,则
,则 的函数关系
的函数关系 的图象可以是( )
的图象可以是( )
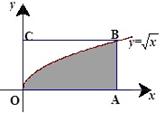
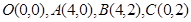 ,曲线
,曲线 经过点
经过点 .现将一质点随机投入长方形
.现将一质点随机投入长方形 中,则质点落在图中阴影区域的概率是()
中,则质点落在图中阴影区域的概率是()