题目内容
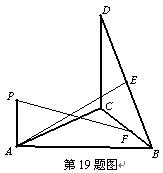
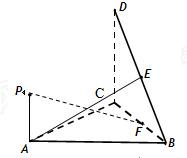 如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点.
如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点.(Ⅰ)证明:AE⊥BC;
(Ⅱ)若点F是线段BC上的动点,设平面PFE与平面PBE所成的平面角大小为θ,当θ在[0,
| π | 4 |
分析:(I)根据题意需要取BC的中点O,连接EO、AO,则由条件证出EO⊥BC和BC⊥AO,根据线面垂直的判定证出BC⊥面AEO,即证出BC⊥AE;
(II)连接PE、EF,根据面BCD⊥面ABC和DC⊥BC证出DC⊥面ABC,由中位线和条件证出四边形APEO为矩形,根据面BCD⊥面ABC和正△ABC证出AO⊥面BCD,即∠PFE为PF与面DBC所成的角,再由PE⊥面BCD证出∠BEF为面PBE与面PFE所成的角,根据θ的范围和条件求出所求的线面角范围.
(II)连接PE、EF,根据面BCD⊥面ABC和DC⊥BC证出DC⊥面ABC,由中位线和条件证出四边形APEO为矩形,根据面BCD⊥面ABC和正△ABC证出AO⊥面BCD,即∠PFE为PF与面DBC所成的角,再由PE⊥面BCD证出∠BEF为面PBE与面PFE所成的角,根据θ的范围和条件求出所求的线面角范围.
解答: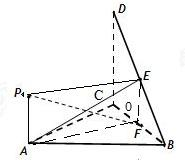 证明:(I)取BC的中点O,连接EO,AO,EO∥DC
证明:(I)取BC的中点O,连接EO,AO,EO∥DC
∵直角△BCD中,DC=BC,∴DC⊥BC,∴EO⊥BC
∵△ABC为等边三角形,∴BC⊥AO,
∵EO∩AO=O,∴BC⊥面AEO,
∴BC⊥AE(4分)
(II)连接PE,连接EF,
∵面BCD⊥面ABC,DC⊥BC,∴DC⊥面ABC,
∵EO∥DC,EO=
DC
∴EO∥PA,EO=PA,故四边形APEO为矩形(5分)
∵面BCD⊥面ABC,AO⊥面BCD,∴PE⊥面BCD,
则∠PFE为PF与面DBC所成的角,(7分)
又∵PE⊥面BCD,∴PE⊥BE,PE⊥EF,
∴∠BEF为面PBE与面PFE所成的角,
即∠BEF=θ∈[0,
],(9分)
此时点F即在线段BO上移动,设DC=BC=2PA=2,
∴EF∈[1,
],tan∠PFE=
=
,
∴
∈[
,
]
∴直线PF与平面DBC所成的角的范围为[arctan
,
].(12分)
 证明:(I)取BC的中点O,连接EO,AO,EO∥DC
证明:(I)取BC的中点O,连接EO,AO,EO∥DC∵直角△BCD中,DC=BC,∴DC⊥BC,∴EO⊥BC
∵△ABC为等边三角形,∴BC⊥AO,
∵EO∩AO=O,∴BC⊥面AEO,
∴BC⊥AE(4分)
(II)连接PE,连接EF,
∵面BCD⊥面ABC,DC⊥BC,∴DC⊥面ABC,
∵EO∥DC,EO=
| 1 |
| 2 |
∴EO∥PA,EO=PA,故四边形APEO为矩形(5分)
∵面BCD⊥面ABC,AO⊥面BCD,∴PE⊥面BCD,
则∠PFE为PF与面DBC所成的角,(7分)
又∵PE⊥面BCD,∴PE⊥BE,PE⊥EF,
∴∠BEF为面PBE与面PFE所成的角,
即∠BEF=θ∈[0,
| π |
| 4 |
此时点F即在线段BO上移动,设DC=BC=2PA=2,
∴EF∈[1,
| 2 |
| PE |
| EF |
| ||
| EF |
∴
| ||
| EF |
|
| 3 |
∴直线PF与平面DBC所成的角的范围为[arctan
| ||
| 2 |
| π |
| 3 |
点评:本题是关于线线、线面和面面垂直与线面角、二面角的综合题,利用垂直的判定(性质)定理,实现线线、线面和面面垂直的相互转化,注意定理中的条件;并且作和证明线面角、二面角时注意利用已知的垂直关系来求作出辅助线,考查了推理论证和逻辑思维能力.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
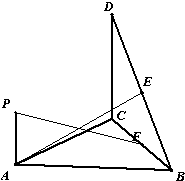 如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E、F分别为DB、CB的中点,
如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E、F分别为DB、CB的中点, (2010•温州一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,为DB的中点,
(2010•温州一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,为DB的中点,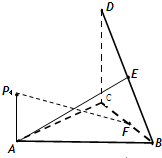 (2012•汕头一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点.
(2012•汕头一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点. ,
, 为DB的中点,
为DB的中点, ,若存在,试确定点F的位置,若不存在,说明理由.
,若存在,试确定点F的位置,若不存在,说明理由.