题目内容
已知f(x)=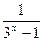 +a为奇函数.
+a为奇函数.
(1)求a的值;
(2)求函数的单调区间.
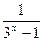 +a为奇函数.
+a为奇函数.(1)求a的值;
(2)求函数的单调区间.
(1)∵f(-x)= +a=
+a= +a=-1+a-
+a=-1+a-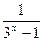 =-1+2a-f(x),
=-1+2a-f(x),
由f(-x)=-f(x),得-1+2a=0,∴a= .
.
(2)对于任意x1≠0,x2≠0,且x1<x2,
f(x1)-f(x2)= ,
,
当x1<x2<0时, >
> ,
, <1,
<1,  <1,
<1,
∴f(x1)-f(x2)>0;
当0<x1<x2时, >
> ,
, >1,
>1, >1,
>1,
∴f(x1)-f(x2)>0.
∴函数的单调递减区间为(-∞,0),(0,+∞).
 +a=
+a= +a=-1+a-
+a=-1+a-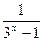 =-1+2a-f(x),
=-1+2a-f(x),由f(-x)=-f(x),得-1+2a=0,∴a=
 .
.(2)对于任意x1≠0,x2≠0,且x1<x2,
f(x1)-f(x2)=
 ,
,当x1<x2<0时,
 >
> ,
, <1,
<1,  <1,
<1,∴f(x1)-f(x2)>0;
当0<x1<x2时,
 >
> ,
, >1,
>1, >1,
>1,∴f(x1)-f(x2)>0.
∴函数的单调递减区间为(-∞,0),(0,+∞).
本题容易出现以下错误:
(1)误认为函数y=a2x+2ax-1在x∈[-1,1]上就是单调增函数,据此得x=1时函数有最大值14,列方程解出a.
(2)令t=ax,x∈[-1,1],不讨论0<a<1还是a>1,就认为t的取值范围是[a-1,a],由此作为外层函数的定义域引出错误.
(1)误认为函数y=a2x+2ax-1在x∈[-1,1]上就是单调增函数,据此得x=1时函数有最大值14,列方程解出a.
(2)令t=ax,x∈[-1,1],不讨论0<a<1还是a>1,就认为t的取值范围是[a-1,a],由此作为外层函数的定义域引出错误.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
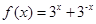 与
与 的定义域均为R,则( )
的定义域均为R,则( ) ,
, 中
中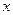 的取值范围.
的取值范围.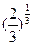 按从小到大的顺序排列.
按从小到大的顺序排列. ,其定义域为_________,值域为_________,奇偶性为_________.
,其定义域为_________,值域为_________,奇偶性为_________. 的解是 .
的解是 .