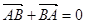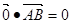题目内容
下列5个命题：
①若3cosx+4sinx=5cos（x+φ），则sinφ=
，cosφ=
；
②函数y=tan(2x+
)关于点(
，0)对称；
③在△ABC中，cosA＞cosB成立的充要条件是A＜B；
④直线x=-
是函数y=sin(2x+
)的图象的一条对称轴；
⑤将函数y=3cos(3x+
)的图象按向量
=(φ，0)平移后的图象关于原点成中心对称，且在(-
，
)上单调递减，则|φ|的最小值为
．
其中正确命题是
①若3cosx+4sinx=5cos（x+φ），则sinφ=
| 4 |
| 5 |
| 3 |
| 5 |
②函数y=tan(2x+
| π |
| 3 |
| π |
| 12 |
③在△ABC中，cosA＞cosB成立的充要条件是A＜B；
④直线x=-
| π |
| 3 |
| π |
| 6 |
⑤将函数y=3cos(3x+
| 3π |
| 4 |
| a |
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
其中正确命题是
③④⑤
③④⑤
．（请将正确命题的序号都填上）分析：①若3cosx+4sinx=5cos（x+φ），则sinφ=-
，cosφ=
；②由当x=
时，y=tan(2x+
)=tan
，不存在，知函数y=tan(2x+
)不能关于点(
，0)对称；③由于余弦函数在（0，π）上是减函数，故A＜B的充要条件为cosA＞cosB；④函数y=sin(2x+
)的图象的对称轴：2x+
=kπ+
，k∈Z，即x=
+
，当k=-1时，为x=-
；⑤函数y=3cos(3x+
)的图象按向量
=(φ，0)平移后的图象关于原点成中心对称，故3（x-φ）+
=
或3（x-φ）+
=
，由平移后的图象y=3cos（3x+
-3φ）在(-
，
)上单调递减，知|φ|的最小值φ=
．
| 4 |
| 5 |
| 3 |
| 5 |
| π |
| 12 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 12 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 6 |
| π |
| 3 |
| 3π |
| 4 |
| a |
| 3π |
| 4 |
| π |
| 2 |
| 3π |
| 4 |
| 3π |
| 2 |
| 3π |
| 4 |
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
解答：解：∵5cos（x+φ）=5cosxcos∅-5sinxsin∅，
∴若3cosx+4sinx=5cos（x+φ），
则sinφ=-
，cosφ=
，故①不正确；
∵当x=
时，y=tan(2x+
)=tan
，不存在，
∴函数y=tan(2x+
)不能关于点(
，0)对称，故②不正确；
在△ABC中，cosA＞cosB成立的充要条件是A＜B，是真命题，
由于余弦函数在（0，π）上是减函数，故A＜B的充要条件为cosA＞cosB，
故③正确；
函数y=sin(2x+
)的图象的对称轴：2x+
=kπ+
，k∈Z，
即x=
+
，当k=-1时，为x=-
，故④正确；
∵函数y=3cos(3x+
)的图象按向量
=(φ，0)平移后的图象关于原点成中心对称，
∴3（x-φ）+
=
或3（x-φ）+
=
，
解得φ=
，或φ=-
．
∵函数y=3cos(3x+
)的图象按向量
=(φ，0)平移后的图象
y=3cos（3x+
-3φ）在(-
，
)上单调递减，
∴|φ|的最小值φ=
，故⑤正确．
故答案为：③④⑤．
∴若3cosx+4sinx=5cos（x+φ），
则sinφ=-
| 4 |
| 5 |
| 3 |
| 5 |
∵当x=
| π |
| 12 |
| π |
| 3 |
| π |
| 2 |
∴函数y=tan(2x+
| π |
| 3 |
| π |
| 12 |
在△ABC中，cosA＞cosB成立的充要条件是A＜B，是真命题，
由于余弦函数在（0，π）上是减函数，故A＜B的充要条件为cosA＞cosB，
故③正确；
函数y=sin(2x+
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
即x=
| kπ |
| 2 |
| π |
| 6 |
| π |
| 3 |
∵函数y=3cos(3x+
| 3π |
| 4 |
| a |
∴3（x-φ）+
| 3π |
| 4 |
| π |
| 2 |
| 3π |
| 4 |
| 3π |
| 2 |
解得φ=
| π |
| 12 |
| π |
| 4 |
∵函数y=3cos(3x+
| 3π |
| 4 |
| a |
y=3cos（3x+
| 3π |
| 4 |
| π |
| 12 |
| π |
| 12 |
∴|φ|的最小值φ=
| π |
| 12 |
故答案为：③④⑤．
点评：本题考查命题的真假判断，解题时要认真审题，注意三角函数的灵活运用．
练习册系列答案
相关题目
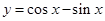的图象向左平移
个单位，所得函数图象关于原点对称；
”,则命题p的否定为：“任意
”；
的零点有2个；
在
处取最小值;
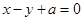与圆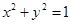
交于不同两点A、B,O为坐标原点，则“
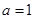”是“向量
满足
”的充分不必要条件.
是两条不同的直线，
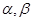是两个不同的平面，给出下列5个命题：
； ②若
；
； ④若
；
、
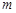是两条不同的直线，
、
是两个不同的平面，给出下列5个命题：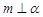
，
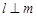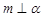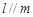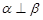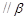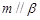，则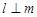
；
，
，
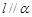，则
；
，
，
，则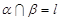
；
，
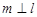，则
，
，则
．
、
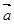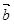都是单位向量，则
；
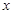轴、
轴都是向量；
