题目内容
3.已知函数f(x)=sin4x+2$\sqrt{3}$sinxcosx-cos4x(1)求函数的最小正周期.
(2)求出该函数在[0,π]上的单调递增区间.
(3)关于x的方程f(x)=k(0<k<2,0≤x≤π)有两个解x1,x2时,求x1+x2.
分析 (1)先根据二倍角公式,化简f(x),再根据最小正周期的定义求出即可,
(2)根据正弦函数的图象和性质即可求出单调递增区间,
(3)利用数形结合得到x1+x2为对称轴的二倍,根据三角函数的性质求出对称轴即可.
解答 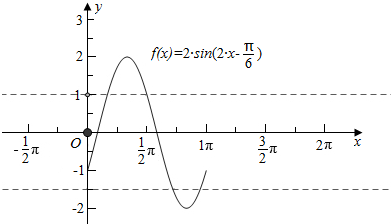 解:(1)f(x)=sin4x+2$\sqrt{3}$sinxcosx-cos4x=(sin2x+cos2x)(sin2x-cos2x)+2$\sqrt{3}$sinxcosx=$\sqrt{3}$sin2x-cos2x=2sin(2x-$\frac{π}{6}$),
解:(1)f(x)=sin4x+2$\sqrt{3}$sinxcosx-cos4x=(sin2x+cos2x)(sin2x-cos2x)+2$\sqrt{3}$sinxcosx=$\sqrt{3}$sin2x-cos2x=2sin(2x-$\frac{π}{6}$),
T=$\frac{2π}{2}$=π,
∴函数的最小正周期为π,
(2)∵-$\frac{π}{2}$+2kπ≤2x-$\frac{π}{6}$≤$\frac{π}{2}$+2kπ,k∈Z,
∴-$\frac{π}{6}$+kπ≤x≤$\frac{π}{3}$+kπ,k∈Z,
当k=0时,-$\frac{π}{6}$≤x≤$\frac{π}{3}$,
当k=1时,$\frac{5π}{6}$≤x≤$\frac{4π}{3}$,
∴函数在[0,π]上的单调递增区间为[0,$\frac{π}{3}$],[$\frac{5π}{6}$,π].
(3)画出函数f(x)的图象,如图所示
x的方程f(x)=k(0<k<2,0≤x≤π)有两个解x1,x2时,
则方程的解位于对称轴两侧,
∵f(x)=2sin(2x-$\frac{π}{6}$)的对称轴为2x-$\frac{π}{6}$=kπ+$\frac{π}{2}$,k∈Z,
∴x=$\frac{π}{3}$+$\frac{kπ}{2}$,k∈Z,
当k=0时,x=$\frac{π}{3}$,
当k=1时,x=$\frac{5π}{6}$,
∴x1+x2=2x=$\frac{2π}{3}$,或x1+x2=2x=$\frac{5π}{3}$.
点评 本题考查三角函数的化简以及正弦函数的图象和性质,培养了学生的运算能力,属于中档题.

| A. | {4,7} | B. | (4,7) | C. | [4,7] | D. | {4,-1} |
| A. | -2 | B. | 2 | C. | -3i | D. | -3 |
| A. | (0,$\frac{1}{2}$] | B. | (0,$\frac{1}{2}$) | C. | (0,$\frac{1}{3}$] | D. | (0,$\frac{1}{3}$) |
 如图所示,从椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上一点M向x轴作垂线,垂足为焦点F1,若椭圆长轴一个端点为A,短轴一个端点为B,且OM∥AB.
如图所示,从椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上一点M向x轴作垂线,垂足为焦点F1,若椭圆长轴一个端点为A,短轴一个端点为B,且OM∥AB.