题目内容
函数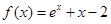 的零点所在的一个区间是
的零点所在的一个区间是
A.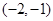 | B.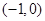 | C. | D.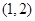 |
C
解析试题分析:判定连续函数在区间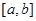 上存在零点的方法
上存在零点的方法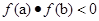 .由
.由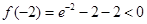 ,
,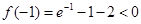 ,
,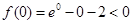 ,
,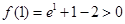 ,
,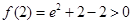 ,所以
,所以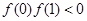 故选C
故选C
考点:函数的零点的判定定理,以及学生的计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设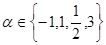 ,则使函数
,则使函数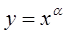 的定义域为R且为奇函数的所有
的定义域为R且为奇函数的所有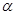 的值为( )
的值为( )
| A.-1,3 | B.-1,1 | C.1,3 | D.-1,1,3 |
设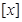 表示不大于
表示不大于 的最大整数,则函数
的最大整数,则函数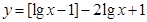 的零点之积为( )
的零点之积为( )
A.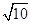 | B.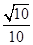 | C.-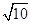 | D.0 |
已知函数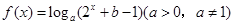 的图象如图所示,则
的图象如图所示,则 满足的关系是( )
满足的关系是( )
A. | B. |
C. | D. |
已知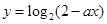 (
(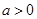 且
且 )在
)在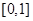 上是
上是 的减函数,则
的减函数,则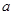 的取值范围是( )
的取值范围是( )
A.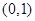 | B.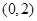 | C.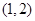 | D.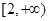 |
若函数 ,则
,则 ( )
( )
A.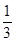 | B.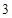 | C.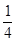 | D.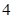 |
已知函数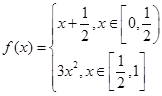 ,若存在
,若存在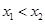 ,使得
,使得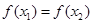 ,则
,则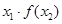 的取值范围为( )
的取值范围为( )
A.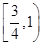 | B.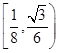 | C.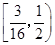 | D.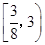 |
.若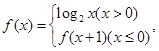 则
则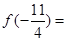 ( )
( )
A.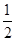 | B.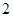 | C.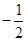 | D.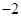 |
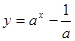
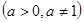 的图象可能是( )
的图象可能是( )