题目内容
设z=1+i+i2+i3+…+i2010,则
=
. | z |
-i
-i
.分析:可利用{in-1}为等比数列,利用等比数列的求和公式结合复数i的幂的性质解决.
解答:解:∵
=i,
∴{in-1}为首项为1,公比为i的等比数列,又i4n=1,i3=-i
∴z=1+i+i2+i3+…+i2010=
=
=
=
=i,
∴
=-i.
| in |
| in-1 |
∴{in-1}为首项为1,公比为i的等比数列,又i4n=1,i3=-i
∴z=1+i+i2+i3+…+i2010=
| 1-i2011 |
| 1-i |
| 1-i3 |
| 1-i |
| 1+i |
| 1-i |
| (1+i)2 |
| (1-i)(1+i) |
∴
. |
| z |
点评:本题考查虚数单位i及其性质,关键是掌握虚数单位i的幂的性质与复数的运算法则,属于中档题.

练习册系列答案
相关题目
设z=1-i(i是虚数单位),则复数
+i2的虚部是( )
| 2 |
| z |
| A、-i | B、-1 | C、i | D、1 |
 =________.
=________.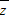 = .
= .