题目内容
下列四个命题中①?x∈R,2x2-x+1>0;
②“x>1且y>2”是“x+y>3”的充要条件;
③函数
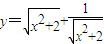 的最小值为2
的最小值为2其中假命题的为 (将你认为是假命题的序号都填上).
【答案】分析:根据二次不等式的解法,我们易判断①的真假;根据充要条件的定义,我们易判断②的对错;利用换元法,结合“对勾”函数的单调性,我们易判断③的正误,进而得到答案.
解答:解:∵2x2-x+1=2(x- )2+
)2+ >0恒成立
>0恒成立
故①?x∈R,2x2-x+1>0为真命题;
若“x>1且y>2”成立,由不等式的性质,我们易得:“x+y>3”
但“x+y>3”时,“x>1且y>2”却不一定成立
故“x>1且y>2”是“x+y>3”的充分不必要条件,故②错误;
令t=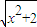 (t≥2)
(t≥2)
则原函数可化为y=t+ (t≥2)
(t≥2)
由函数y=t+ 的单调性易知,[2,+∞)为函数的单调递增区间
的单调性易知,[2,+∞)为函数的单调递增区间
故当t=2时,y有最小值 ,故③错误.
,故③错误.
故答案为:②③
点评:本题考查的知识点是命题的真假判断与应用,其中利用不等式的解法,充要条件的定义,函数的单调性,分别判断三个命题的真假是解答的关键.
解答:解:∵2x2-x+1=2(x-
 )2+
)2+ >0恒成立
>0恒成立故①?x∈R,2x2-x+1>0为真命题;
若“x>1且y>2”成立,由不等式的性质,我们易得:“x+y>3”
但“x+y>3”时,“x>1且y>2”却不一定成立
故“x>1且y>2”是“x+y>3”的充分不必要条件,故②错误;
令t=
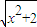 (t≥2)
(t≥2)则原函数可化为y=t+
 (t≥2)
(t≥2)由函数y=t+
 的单调性易知,[2,+∞)为函数的单调递增区间
的单调性易知,[2,+∞)为函数的单调递增区间故当t=2时,y有最小值
 ,故③错误.
,故③错误.故答案为:②③
点评:本题考查的知识点是命题的真假判断与应用,其中利用不等式的解法,充要条件的定义,函数的单调性,分别判断三个命题的真假是解答的关键.

练习册系列答案
相关题目
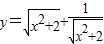 的最小值为2
的最小值为2