题目内容
设a>0,求函数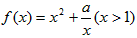 的单调区间,并且如果有极值时,求出极值。
的单调区间,并且如果有极值时,求出极值。
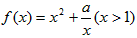 的单调区间,并且如果有极值时,求出极值。
的单调区间,并且如果有极值时,求出极值。解:∵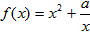 ,
,
∴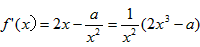
令f′(x)=0,得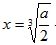 ,
,
因此,函数在(1,+∞)内的单调区间以及是否有极值均与a有关系,要视x= 与x=1的大小关系而定,
与x=1的大小关系而定,
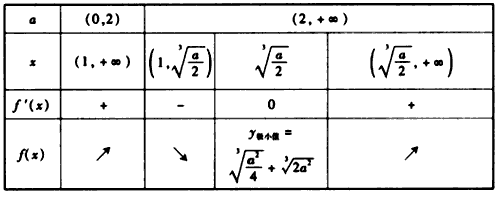
综上可知,
(1)若a≤2,则函数在(1,+∞)上单调递增,无极值;
(2)若a>2,则函数在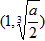 上递减,在
上递减,在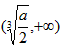 上递增,在x=
上递增,在x=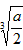 处取得极小值,即函数的极小值为f
处取得极小值,即函数的极小值为f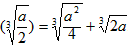 。
。
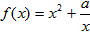 ,
,∴
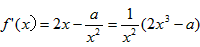
令f′(x)=0,得
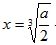 ,
,因此,函数在(1,+∞)内的单调区间以及是否有极值均与a有关系,要视x=
 与x=1的大小关系而定,
与x=1的大小关系而定,
综上可知,
(1)若a≤2,则函数在(1,+∞)上单调递增,无极值;
(2)若a>2,则函数在
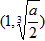 上递减,在
上递减,在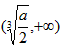 上递增,在x=
上递增,在x=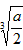 处取得极小值,即函数的极小值为f
处取得极小值,即函数的极小值为f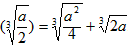 。
。 
练习册系列答案
相关题目
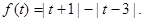
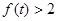 的解集;
的解集;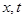 ,均有
,均有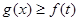 恒成立,求a的取值范围。
恒成立,求a的取值范围。