题目内容
(21)已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C上的点到焦点距离的最大值为3,最小值为1.(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l:y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点,求证:直线l过定点,并求出该定点的坐标.
解:(Ⅰ)由题意设椭圆的标准方程为![]() =1(a>b>0),
=1(a>b>0),
由已知得:a+c=3,a-c=1,
∴a=2,c=1,
∴b2=a2-c2=3.
∴椭圆的标准方程为![]() =1.
=1.
(Ⅱ)设A(x1,y1),B(x2,y2),
联立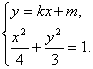
得(3+4k2)x2+8mkx+4(m2-3)=0,

又y1y2=(kx1+m)(kx2+m)=k2x1x2+mk(x1+x2)+m2=![]() ,
,
因为以AB为直径的圆过椭圆右顶点D(2,0),
∴kACkAD=-1,则![]() = -1.
= -1.
∴y1y2+x1x2-2(x1+x2)+4=0.
∴![]() +4=0.
+4=0.
∴7m2+16mk+4k2=0.
解得:
m1=-2k,m2=![]() ,且均满足3+4k2-m2>0.
,且均满足3+4k2-m2>0.
当m1=-2k时,l的方程为y=k(x-2),直线过定点(2,0),与已知矛盾;
当m2=![]() 时,l的方程为y=k(x
时,l的方程为y=k(x![]() ),直线过定点(
),直线过定点(![]() ,0).
,0).
所以,直线l过定点,定点坐标为(![]() ,0).
,0).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
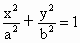 (a>b>0)的离心率为
(a>b>0)的离心率为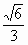 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为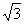 .
.
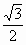 ,求△AOB面积的最大值.
,求△AOB面积的最大值.