题目内容
过坐标原点O作单位圆 的两条互相垂直的半径
的两条互相垂直的半径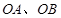 ,若在该圆上存在一点
,若在该圆上存在一点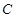 ,使得
,使得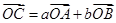 (
( ),则以下说法正确的是( )
),则以下说法正确的是( )
A.点 一定在单位圆内 一定在单位圆内 |
B.点 一定在单位圆上 一定在单位圆上 |
C.点 一定在单位圆外 一定在单位圆外 |
D.当且仅当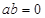 时,点 时,点 在单位圆上 在单位圆上 |
B.
解析试题分析:使用特殊值方法求解.设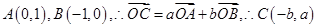 .
. 在圆上,
在圆上, 在单位圆上,故选B.
在单位圆上,故选B.
考点:1.平面向量基本定理;2.点和圆的位置关系.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
已知 ,
, 且
且 ∥
∥ ,则
,则 ( )
( )
| A.-3 | B. | C.0 | D. |
已知平面向量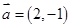 ,
,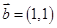 ,
,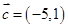 . 若
. 若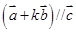 ,则实数
,则实数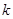 的值为( )
的值为( )
A.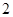 | B.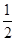 | C.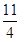 | D.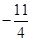 |
若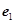 ,
,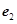 是平面内的一组基底,则下列四组向量不能作为平面向量的基底的是( )
是平面内的一组基底,则下列四组向量不能作为平面向量的基底的是( )
A.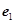 + +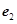 和 和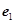 - -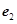 | B.3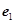 -2 -2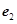 和-6 和-6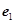 +4 +4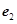 |
C.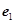 +2 +2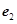 和2 和2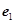 + +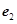 | D.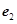 和 和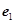 + +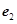 |
已知平面向量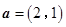 ,
,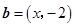 ,若
,若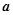 ∥
∥ ,则
,则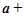
 等于( )
等于( )
A.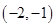 | B.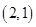 | C.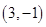 | D.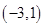 |
已知两点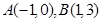 ,向量
,向量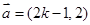 ,若
,若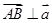 ,则实数
,则实数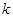 的值为( )
的值为( )
| A.-2 | B.﹣l | C.1 | D.2 |
设x,y∈R,向量a=(x,1),b=(1,y),c=(2,-4),且a⊥c,b∥c,则|a+b|= ( ).
A.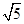 | B.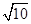 | C.2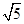 | D.10 |
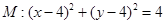 ,四边形ABCD为圆
,四边形ABCD为圆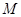 的内接正方形,E,F分别为边AB,AD的中点,当正方形ABCD绕圆心
的内接正方形,E,F分别为边AB,AD的中点,当正方形ABCD绕圆心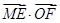 的取值范围是( )
的取值范围是( )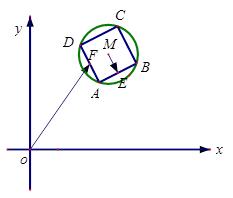
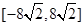
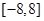
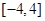
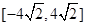
 ,则k的值为( )
,则k的值为( )
