题目内容
在等差数列 中,已知
中,已知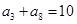 ,则
,则 =( )
=( )
| A.10 | B.18 | C.20 | D.28 |
C
解析试题分析:因为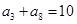 ,所以由等差数列的性质,得
,所以由等差数列的性质,得 ,
,
所以 =
= ,选C.
,选C.
考点:等差数列的性质

练习册系列答案
相关题目
数列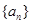 满足:
满足: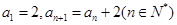 ,则其前10项的和
,则其前10项的和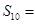 ( )
( )
| A.100 | B.101 | C.110 | D.111 |
已知等差数列 中,
中, , 则
, 则 的值是( )
的值是( )
| A.15 | B.30 | C.31 | D.64 |
设 是等差数列
是等差数列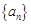 的前
的前 项和,若
项和,若 ,则
,则 ( )
( )
| A.1 | B.-1 | C.2 | D.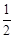 |
已知数列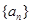 ,若点
,若点
 均在直线
均在直线 上,则数列
上,则数列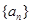 的前9项和
的前9项和 等于( )
等于( )
| A.18 | B.20 | C.22 | D.24 |
若数列{an}是等差数列,则数列{bn}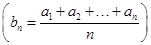 也为等差数列.类比这一性质可知,若正项数列{cn}是等比数列,且{dn}也是等比数列,则dn的表达式应为( )
也为等差数列.类比这一性质可知,若正项数列{cn}是等比数列,且{dn}也是等比数列,则dn的表达式应为( )
A.dn=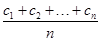 | B.dn=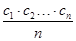 |
C.dn= 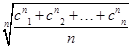 | D.dn=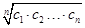 |
在等差数列{an}中,首项a1=120,公差d=-4,若Sn≤an(n≥2),则n的最小值为( )
| A.60 | B.62 | C.70 | D.72 |
已知数列{an}是公差为2的等差数列,且a1,a2,a5成等比数列,则数列{an}的前5项和S5=( )
| A.20 | B.30 | C.25 | D.40 |
设等差数列{an}的前n项和为Sn,Sm-1=-2,Sm=0,Sm+1=3,则m等于( ).
| A.3 | B.4 | C.5 | D.6 |