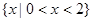题目内容
已知: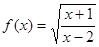 的定义域为A,
的定义域为A,
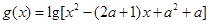 的定义域为B。
的定义域为B。
(Ⅰ)求集合A与B;
(Ⅱ)若A∪B=B,求实数a 的取值范围.
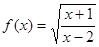 的定义域为A,
的定义域为A,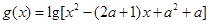 的定义域为B。
的定义域为B。(Ⅰ)求集合A与B;
(Ⅱ)若A∪B=B,求实数a 的取值范围.
(Ⅰ)A={x|x≤-1或x>2},B={x|x<a或x>a+1}(Ⅱ)(-1,1]
本试题主要是考查了集合的运算以及函数定义域的综合运用。
(1))由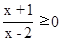 且x-2≠0得A={x|x≤-1或x>2}
且x-2≠0得A={x|x≤-1或x>2}
由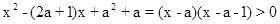 得B={x|x<a或x>a+1},
得B={x|x<a或x>a+1},
(2)由A∪B=B知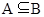 ,那么可知
,那么可知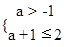 得到结论。
得到结论。
解:(1)由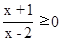 且x-2≠0得A={x|x≤-1或x>2}………………………(3分)
且x-2≠0得A={x|x≤-1或x>2}………………………(3分)
由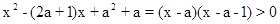 得B={x|x<a或x>a+1}…(6分)
得B={x|x<a或x>a+1}…(6分)
(2)由A∪B=B知 …………………… (8分)
…………………… (8分)
∴由(1)得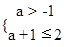 即-1<a≤1……………………(12分)
即-1<a≤1……………………(12分)
∴实数a的取值范围是(-1,1] ………………(13分)
(1))由
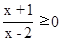 且x-2≠0得A={x|x≤-1或x>2}
且x-2≠0得A={x|x≤-1或x>2}由
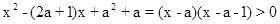 得B={x|x<a或x>a+1},
得B={x|x<a或x>a+1},(2)由A∪B=B知
 ,那么可知
,那么可知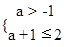 得到结论。
得到结论。解:(1)由
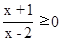 且x-2≠0得A={x|x≤-1或x>2}………………………(3分)
且x-2≠0得A={x|x≤-1或x>2}………………………(3分)由
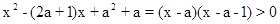 得B={x|x<a或x>a+1}…(6分)
得B={x|x<a或x>a+1}…(6分)(2)由A∪B=B知
 …………………… (8分)
…………………… (8分)∴由(1)得
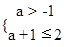 即-1<a≤1……………………(12分)
即-1<a≤1……………………(12分)∴实数a的取值范围是(-1,1] ………………(13分)

练习册系列答案
相关题目
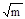 },集合B={1,m}.若A∩B=B,则实数m= .
},集合B={1,m}.若A∩B=B,则实数m= . =y,x
=y,x ,集合N={y︱x+y=0,x
,集合N={y︱x+y=0,x },则M
},则M N等于
N等于 0}
0}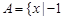 ≤x≤2},B=
≤x≤2},B= ,则
,则 =( )
=( )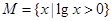 ,
, ,则
,则 ( )
( ) 



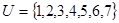 ,
,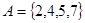 ,
,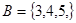 ,则
,则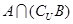 =( )
=( )
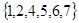
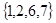
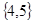
 ,集合
,集合 则集合
则集合 =( )
=( )



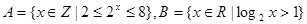 ,则
,则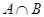 =__________.
=__________.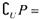 ( )
( )