题目内容
如图,已知各顶点都在半球面上的正三棱锥S-ABC.若AB=a,则该三棱锥的体积为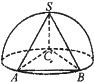
分析:根据三棱锥的各顶点都在半球面上的正三棱锥S-ABC.且AB=a,我们根据圆内接三角形的性质,我们易得到棱锥底面的外接圆即为“赤道”,其中半径等于球半径,高等于球半径,求出高和底面面积后,代入棱锥体积公式,即可得到答案.
解答:解:若正三棱锥S-ABC的各顶点都在半球面上
则等边△ABC的外接圆半径等于球半径R
又∵AB=a,∴R=
a
则S△ABC=(
×1×
)a2=
a2
∴V=
×S△ABC×R=
故答案为:
则等边△ABC的外接圆半径等于球半径R
又∵AB=a,∴R=
| ||
| 3 |
则S△ABC=(
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
∴V=
| 1 |
| 3 |
| a3 |
| 12 |
故答案为:
| a3 |
| 12 |
点评:本题考查的知识点是棱锥的体积公式,其中根据球的几何特征和棱锥的几何特征,求出棱锥的高和底面面积,是解答本题的关键.

练习册系列答案
相关题目



