题目内容
(2010•珠海二模)甲乙两艘船都要在某个泊停靠,若分别停靠6小时、8小时.假定它们在一昼夜的时间段内任意时刻到达,则这两艘船中有一艘在停靠泊位时必须等待的概率为
.
| 143 |
| 288 |
| 143 |
| 288 |
分析:先设甲到x点,乙到y点,建立甲先到,乙先到满足的条件,再画出并求解0<x<24,0<y<24可行域面积,求出满足条件的可行域面积,由概率公式求解.
解答: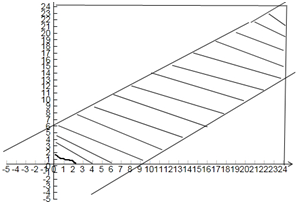 解:设甲到x点,乙到y点,若甲先到乙等待需满足x+6>y,若乙先到甲等待需满足y+8>x.
解:设甲到x点,乙到y点,若甲先到乙等待需满足x+6>y,若乙先到甲等待需满足y+8>x.
满足0<x<24,0<y<24可行域面积s=576
满足x+6>y,y+8>x的面积为
576-
×18×18-
×16×16=286;
这两艘船中至少有一艘在停靠泊位时必须等待的概率为:
故答案为:
 解:设甲到x点,乙到y点,若甲先到乙等待需满足x+6>y,若乙先到甲等待需满足y+8>x.
解:设甲到x点,乙到y点,若甲先到乙等待需满足x+6>y,若乙先到甲等待需满足y+8>x.满足0<x<24,0<y<24可行域面积s=576
满足x+6>y,y+8>x的面积为
576-
| 1 |
| 2 |
| 1 |
| 2 |
这两艘船中至少有一艘在停靠泊位时必须等待的概率为:
| 143 |
| 288 |
故答案为:
| 143 |
| 288 |
点评:本题主要考查建模,解模能力,考查学生分析解决问题的能力,涉及到可行域的画法及其面积的求法,属于中档题.

练习册系列答案
相关题目
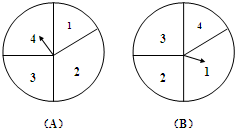 (2010•珠海二模)如图是两个独立的转盘(A)、(B),在两个图中的四个扇形区域的圆心角分别为60°、120°、90°90°.用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域数为x,转盘(B)指针所对的区域数为y,x、y∈{1,2,3,4},设x+y的值为ξ,每一次游戏得到奖励分为ξ.
(2010•珠海二模)如图是两个独立的转盘(A)、(B),在两个图中的四个扇形区域的圆心角分别为60°、120°、90°90°.用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域数为x,转盘(B)指针所对的区域数为y,x、y∈{1,2,3,4},设x+y的值为ξ,每一次游戏得到奖励分为ξ.