题目内容
已知直线5x+12y+m=0与圆x2-2x+y2=0相切，则m=________．
8或-18
分析：根据直线与圆相切的性质可知圆心直线的距离为半径，先把圆的方程整理的标准方程求得圆心和半径，在利用点到直线的距离求得圆心到直线的距离为半径，求得答案．
解答：整理圆的方程为（x-1）2++y2=1
故圆的圆心为（1，0），半径为1
直线与圆相切
∴圆心到直线的距离为半径
即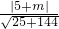
=1，求得m=8或-18
故答案为：8或-18
点评：本题主要考查了直线与圆的位置关系．解题的过程充分利用数形结合的思想和直线与圆相切的性质．
分析：根据直线与圆相切的性质可知圆心直线的距离为半径，先把圆的方程整理的标准方程求得圆心和半径，在利用点到直线的距离求得圆心到直线的距离为半径，求得答案．
解答：整理圆的方程为（x-1）2++y2=1
故圆的圆心为（1，0），半径为1
直线与圆相切
∴圆心到直线的距离为半径
即
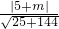=1，求得m=8或-18故答案为：8或-18
点评：本题主要考查了直线与圆的位置关系．解题的过程充分利用数形结合的思想和直线与圆相切的性质．
练习册系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目