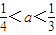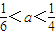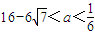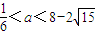题目内容
已知a,b,c是正实数,且abc+a+c=b,设p=
-
+
,则p的最大值为
.
| 2 |
| a2+1 |
| 2 |
| b2+1 |
| 3 |
| c2+1 |
| 10 |
| 3 |
| 10 |
| 3 |
分析:设a=tanα,b=tanβ,c=tanγ,α,β,γ∈(0,
),然后将p利用同角三角函数关系进行化简,根据条件可求出角α、β、γ的等量关系,最后利用二次函数的性质求出最值即可.
| π |
| 2 |
解答:解:设a=tanα,b=tanβ,c=tanγ,α,β,γ∈(0,
),
则p=2cos2α-2cos2β+3cos2γ=cos2α-cos2β+3cos2γ=2sin(α+β)sin(β-α)+3cos2γ.
由abc+a+c=b得b=
即tanβ=
=tan(α+γ),又α,β,γ∈(0,
),
所以β=α+γ,β-α=γ,p=2sin(α+β)sin(β-α)+3cos2γ=2sin(α+β)sinγ+3cos2γ≤2sinγ+3cos2γ=
-3(sinγ-
)2≤
.
当α+β=
,sinγ=
时取等号.
所以p=
-
+
的最大值为
故答案为:
| π |
| 2 |
则p=2cos2α-2cos2β+3cos2γ=cos2α-cos2β+3cos2γ=2sin(α+β)sin(β-α)+3cos2γ.
由abc+a+c=b得b=
| a+c |
| 1-ac |
即tanβ=
| tanα+tanγ |
| 1-tanαtanγ |
| π |
| 2 |
所以β=α+γ,β-α=γ,p=2sin(α+β)sin(β-α)+3cos2γ=2sin(α+β)sinγ+3cos2γ≤2sinγ+3cos2γ=
| 10 |
| 3 |
| 1 |
| 3 |
| 10 |
| 3 |
当α+β=
| π |
| 2 |
| 1 |
| 3 |
所以p=
| 2 |
| a2+1 |
| 2 |
| b2+1 |
| 3 |
| c2+1 |
| 10 |
| 3 |
故答案为:
| 10 |
| 3 |
点评:本题主要考查了基本不等式的应用,以及三角换元和同角三角函数和和差化积等公式,同时考查了运算求解的能力,属于中档题.

练习册系列答案
相关题目

 ,关于方程
,关于方程 (
( 为正实数)的根的叙述有下列四个命题
为正实数)的根的叙述有下列四个命题 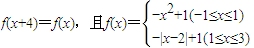 ,若方程f(x)-ax=0有5个实根,则正实数a的取值范围是( )
,若方程f(x)-ax=0有5个实根,则正实数a的取值范围是( )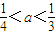
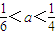
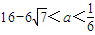
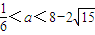
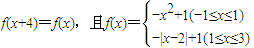 ,若方程f(x)-ax=0有5个实根,则正实数a的取值范围是( )
,若方程f(x)-ax=0有5个实根,则正实数a的取值范围是( )