题目内容
若圆的方程为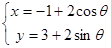 (
(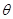 为参数),直线的方程为
为参数),直线的方程为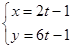 (t为参数),则直线与圆的位置关系是( )。
(t为参数),则直线与圆的位置关系是( )。
| A.相交过圆心 | B.相交而不过圆心 | C.相切 | D.相离 |
B
解析试题分析: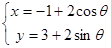 即
即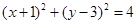 ,
,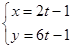 即
即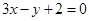 ,研究圆心(-1,3)到直线
,研究圆心(-1,3)到直线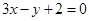 距离
距离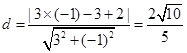 <2,所以,直线与圆的位置关系是相交而不过圆心,选B。
<2,所以,直线与圆的位置关系是相交而不过圆心,选B。
考点:简单曲线的参数方程,直线与圆的位置关系。
点评:中档题,首先将参数方程转化成普通方程,利用几何法,研究关系。也可以利用代数法,研究方程组解的情况。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知直线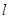 的参数方程为
的参数方程为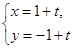 (
(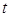 为参数),则直线
为参数),则直线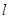 的普通方程为( )
的普通方程为( )
A.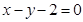 | B.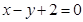 | C.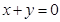 | D.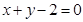 |
与参数方程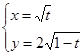
 (
(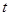 为参数)等价的普通方程为( )
为参数)等价的普通方程为( )
A.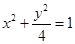 | B.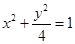 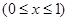 |
C.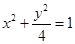 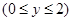 | D.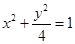 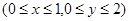 |
参数方程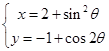 (
( 为参数)化成普通方程是
为参数)化成普通方程是
A.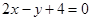 | B.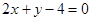 |
C.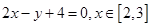 | D.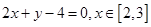 |
设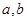 是方程x
是方程x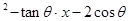 =0的两个实根,那么过点
=0的两个实根,那么过点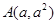 和
和 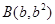 (
(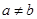 )的直线与曲线
)的直线与曲线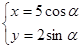 (
(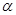 为参数)的位置关系是
为参数)的位置关系是
| A.相交 | B.相切 | C.相交或相切 | D.相离 |
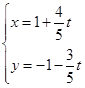 (
(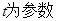 )被曲线
)被曲线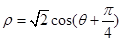 所截的弦长 .
所截的弦长 .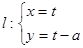 (t为参数)过椭圆C:
(t为参数)过椭圆C: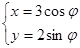 (
( 为参数)的右顶点,则常数a的值为______.
为参数)的右顶点,则常数a的值为______.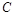 :
: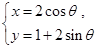 (
(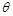 为参数)的圆心坐标为__________;直线
为参数)的圆心坐标为__________;直线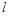 :
: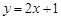 被圆
被圆 ,PO=12.求⊙O的半径。
,PO=12.求⊙O的半径。