Question

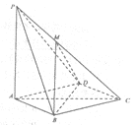
【题目】已知椭圆：，过原点作射线交椭圆于，平行四边形的顶点，在椭圆上.

（1）若射线的斜率为，求直线的斜率；

（2）求证：四边形的面积为定值.

Answer 1

【答案】（1）；（2）证明见解析.

【解析】

（1）将射线方程与椭圆方程联立可求得点坐标，由此得到中点坐标，利用点差法可求得直线斜率；

（2）①当直线斜率不存在时，由对称性可知四边形为菱形，可求得其面积为；②当直线斜率存在时，设方程为，与椭圆方程联立得到韦达定理的形式，结合平面向量线性运算可求得点坐标，代入椭圆方程得到的关系；利用弦长公式和点到直线距离公式表示出和原点到直线距离，由化简可得面积为；综合两种情况可得结论.

（1）设射线的方程为，与椭圆联立得：，

当时，中点，

四边形为平行四边形，为中点，

设，，

，两式作差得：，

；

当时，同理可求得；

综上所述：直线的斜率为.

（2）①当直线斜率不存在时，四边形为菱形，且平分，

方程为或，，；

②当直线斜率存在时，设方程为：，

由得：，

则，整理得：，

设，，则，，

，

四边形为平行四边形，，

即点坐标为，即，

在椭圆上，，整理得：，

，

又原点到直线距离，；

综上所述：四边形的面积为定值.