题目内容
定义![]()
![]() 为有限项数列
为有限项数列![]() 的波动强度.
的波动强度.
(Ⅰ)当![]() 时,求
时,求![]() ;
;
(Ⅱ)若数列![]() 满足
满足![]() ,求证:
,求证:![]() ;
;
(Ⅲ)设![]() 各项均不相等,且交换数列
各项均不相等,且交换数列![]() 中任何相邻两项的位置,都会使数列的波动强度增加,求证:数列
中任何相邻两项的位置,都会使数列的波动强度增加,求证:数列![]() 一定是递增数列或递减数列.
一定是递增数列或递减数列.
(Ⅰ)解:![]() ………………1分
………………1分
![]() . ………………3分
. ………………3分
(Ⅱ)证明:因为![]() ,
,
![]() ,
,
所以![]() . ……4分
. ……4分
因为![]() ,所以
,所以![]() ,或
,或![]() .
.
若![]() ,则
,则![]()
![]()
当![]() 时,上式
时,上式![]() ,
,
当![]() 时,上式
时,上式![]() ,
,
当![]() 时,上式
时,上式![]() ,
,
即当![]() 时,
时,![]() . ………………6分
. ………………6分
若![]() ,
,
则![]() ,
,
![]() .(同前)
.(同前)
所以,当![]() 时,
时,![]() 成立. ……………7分
成立. ……………7分
(Ⅲ)证明:由(Ⅱ)易知对于四个数的数列,若第三项的值介于前两项的值之间,则交换第二项与第三项的位置将使数列波动强度减小或不变.(将此作为引理)
下面来证明当![]() 时,
时,![]() 为递减数列.
为递减数列.
(ⅰ)证明![]() .
.
若![]() ,则由引理知交换
,则由引理知交换![]() 的位置将使波动强度减小或不变,与已知矛盾.
的位置将使波动强度减小或不变,与已知矛盾.
若![]() ,则
,则![]() ,与已知矛盾.
,与已知矛盾.
所以,![]() . ………………9分
. ………………9分
(ⅱ)设![]() ,证明
,证明![]() .
.
若![]() ,则由引理知交换
,则由引理知交换![]() 的位置将使波动强度减小或不变,与已知矛盾.
的位置将使波动强度减小或不变,与已知矛盾.
若![]() ,则
,则![]() ,与已知矛盾.
,与已知矛盾.
所以,![]() . …………11分
. …………11分
(ⅲ)设![]() ,证明
,证明![]() .
.
若![]() ,考查数列
,考查数列![]() ,
,
则由前面推理可得![]() ,与
,与![]() 矛盾.
矛盾.
所以,![]() . ……………12分
. ……………12分
综上,得证.
同理可证:当![]() 时,有
时,有![]() 为递增数列. ………………13分
为递增数列. ………………13分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 为有限项数列
为有限项数列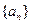 的波动强度.
的波动强度.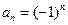 时,求
时,求 ;
;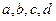 满足
满足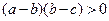 ,求证:
,求证: ;
;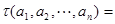
 为有限项数列
为有限项数列 的波动强度.
的波动强度. 时,求
时,求 ;
; 满足
满足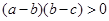 ,求证:
,求证: ;
;