题目内容
曲线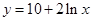 在点
在点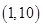 处的切线方程是
处的切线方程是
A.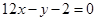 B.
B.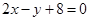
C.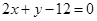 D.
D.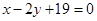
【答案】
B
【解析】
试题分析:根据题意研究的是曲线在某点出的切线方程,因此可知切点为(1,10),那么函数f(x)= 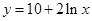 的导数为f’(x)=
的导数为f’(x)=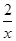 ,那么可知在x=1处的导数值为2,即为切线的斜率,因此利用点斜式方程得到为y-10=2(x-1),变形得到为
,那么可知在x=1处的导数值为2,即为切线的斜率,因此利用点斜式方程得到为y-10=2(x-1),变形得到为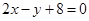 ,故选B.
,故选B.
考点:本试题考查了导数的几何意义的运用。
点评:利用导数求解曲线的切线方程要注意两点:第一就是切点是谁?第二就是切线的斜率,也就是切点的导数值,然后利用点斜式方程得到结论。属于基础题。

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 ,其中
,其中
 在点
在点 处的切线方程为
处的切线方程为 ,求函数
,求函数 的解析式;
的解析式; ,不等式
,不等式 在
在 上恒成立,求实数b的取值范围。
上恒成立,求实数b的取值范围。 ,
, 在点
在点 处
处 的切线方程;
的切线方程; 的导数
的导数 满足
满足 ,
, ,其中常数
,其中常数 ,求曲线
,求曲线 在点
在点 处的切线方程.
处的切线方程.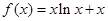 在点
在点 处的切线方程为 .
处的切线方程为 .