题目内容
已知F1、F2是双曲线 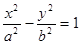 (a>0,b>0)的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是 ( )
(a>0,b>0)的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是 ( )
A.4+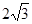 | B.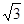 +1 +1 | C.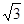 —1 —1 | D.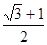 |
B
解析考点:双曲线的简单性质.
分析:先根据双曲线方程求得焦点坐标的表达式,进而可求得三角形的高,则点M的坐标可得,进而求得其中点N的坐标,代入双曲线方程求得a,b和c的关系式化简整理求得关于e的方程求得e.
解:依题意可知双曲线的焦点为F1(-c,0),F2(c,0)
∴F1F2=2c
∴三角形高是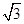 c
c
M(0,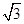 c)
c)
所以中点N(-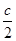 ,
,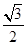 c)
c)
代入双曲线方程得: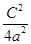 -
-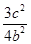 =1
=1
整理得:b2c2-3a2c2=4a2b2
∵b2=c2-a2
所以c4-a2c2-3a2c2=4a2c2-4a4
整理得e4-8e2+4=0
求得e2=4±2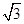
∵e>1,
∴e=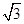 +1
+1
故选B

练习册系列答案
相关题目
已知双曲线 ,则p的值为( )
,则p的值为( )
| A.-2 | B.-4 | C.2 | D.4 |
椭圆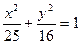 的焦点为F1,F
的焦点为F1,F 2,P为椭圆上一点,若
2,P为椭圆上一点,若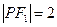 ,则
,则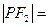
| A.2 | B.4 | C.6 | D.8 |
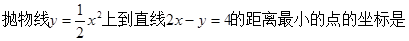 ( )
( )
| A.(1,1) | B.(1,2) | C.(2,2) | D.(2,4) |
已知抛物线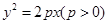 ,过点
,过点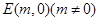 的直线交抛物线于点M、N,交y轴于点P,若
的直线交抛物线于点M、N,交y轴于点P,若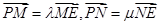 ,则
,则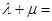 ( )
( )
| A.1 | B.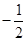 | C.-1 | D.-2 |
焦点为F(0,10),渐近线方程为4x±3y=0的双曲线的方程是 ( )
A.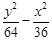 =1 =1 | B.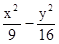 =1 =1 | C.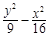 ="1" ="1" | D.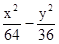 =1 =1 |
一条动圆圆心在抛物线上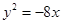 ,动圆恒过点(-2,0)则下列哪条直线是动圆的公切线()
,动圆恒过点(-2,0)则下列哪条直线是动圆的公切线()
| A.x=4 | B.y=4 | C.x=2 | D.x=-2 |
F1、F2分别是椭圆 的左、右焦点,点P在椭圆上,线段PF2与
的左、右焦点,点P在椭圆上,线段PF2与 轴的交点为
轴的交点为
M,且 ,则点M到坐标原点O的距离是
,则点M到坐标原点O的距离是
A. | B.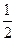 | C.1 | D.2 |
 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则p的值为
的右焦点重合,则p的值为
