Question

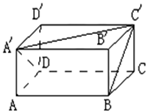
如图，已知长方体的长宽都是4cm，高为2cm．
（1）求BC与A′C′，A′D与BC′所成角的余弦值；
（2）求AA′与BC，AA′与CC′所成角的大小．

Answer 1

分析：（1）根据长方体的性质，可得∠A'C'B'就是异面直线BC与A′C′所成角，在Rt△A'B'C'中，利用三角函数的定义可得cos∠A'C'B'=

2

2

，即为BC与A′C′所成角的余弦值．同理可得直线B'C与BC'所成的角就是A′D与
BC′所成的角，结合余弦定理加以计算即可得到A′D与BC′所成角的余弦值；
（2）根据长方体的性质可得AA'∥BB'，因此矩形BB'C'C中，∠B'BC=90°就是AA′与BC所成的角；再由AA′∥CC′，得到AA′与CC′所成角为0°．

解答：解：（1）∵长方体ABCD-A'B'C'D'中，BC∥A′C′
∴∠A'C'B'就是异面直线BC与A′C′所成角
Rt△A'B'C'中，A′C′=

42+42

=4

2

∴cos∠A'C'B'=

B’C‘

A′C′

=

2

2

；
连结B'C，可得四边形A'DCB'是平行四边形，
∴A'D∥CB'，直线B'C与BC'所成的角就是A′D与BC′所成的角
矩形BB'C'C中，BC'=B'C=

42+22

=2

5

设A′D与BC′所成的角为θ，则由余弦定理得
cosθ=|

5+5-16

2× 5 × 5

|=

3

5

综上所述，可得BC与A′C′，A′D与BC′所成角的余弦值分别为

2

2

和

3

5

；
（2）∵长方体ABCD-A'B'C'D'中，AA'∥BB'
∴∠B'BC（或其补角）就是AA′与BC所成的角
矩形BB'C'C中，可得∠B'BC=90°；
又∵AA′∥CC′，∴AA′与CC′所成角为0°
综上所述AA′与BC，AA′与CC′所成角的大小分别为90°和0°．

点评：本题在长方体中求异面直线所成的角，着重考查了长方体的性质、直角三角形中三角函数的定义和异面直线所成角的定义等知识，属于基础题．