题目内容
甲乙两个袋子中,各放有大小和形状、个数相同的小球若干.每个袋子中标号为0的小球为1个,标号为1的2个,标号为2的n个.从一个袋子中 任取两个球,取到的标号都是2的概率是 ;
;
(1)从甲袋中任取两个球,标号分别是1和2的取法有多少种?
(2)从甲袋中任取两个球,已知其中一个的标号是1的条件下,求另一个标号也是1的概率;
(3)从两个袋子中各取一个小球,用ξ表示这两个小球的标号之和,求ξ的分布列和E(ξ).
解:(1)由题意得: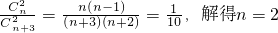 ;
;
记“从甲袋中任取两个球,标号分别是1和2”为事件M,则M的总数是C21=2.
所以从甲袋中任取两个球,标号分别是1和2的取法有2种.
(2)记“一个标号是1”为事件A,“另一个标号也是1”为事件B,
所以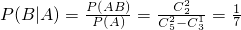
(3)随机变量ξ的分布列为
Eξ=2.4
分析:(1)由题意得:n=2;记“从甲袋中任取两个球,标号分别是1和2”为事件M,则M的总数是C21=2.
(2)记“一个标号是1”为事件A,“另一个标号也是1”为事件B,所以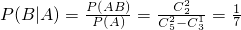
(3)由题意得画出变量的分布列运用公式可得Eξ=2.4.
点评:解决此类问题的关键是应用排列组合的总数准确的基本事件的总数与符合条件事件所包含的结果数,再利用概率公式进行计算.
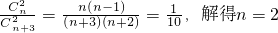 ;
;记“从甲袋中任取两个球,标号分别是1和2”为事件M,则M的总数是C21=2.
所以从甲袋中任取两个球,标号分别是1和2的取法有2种.
(2)记“一个标号是1”为事件A,“另一个标号也是1”为事件B,
所以
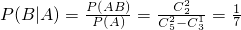
(3)随机变量ξ的分布列为
| ξ | 0 | 1 | 2 | 3 | 4 |
| P |  |  | 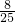 | 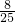 |  |
分析:(1)由题意得:n=2;记“从甲袋中任取两个球,标号分别是1和2”为事件M,则M的总数是C21=2.
(2)记“一个标号是1”为事件A,“另一个标号也是1”为事件B,所以
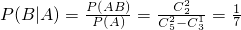
(3)由题意得画出变量的分布列运用公式可得Eξ=2.4.
点评:解决此类问题的关键是应用排列组合的总数准确的基本事件的总数与符合条件事件所包含的结果数,再利用概率公式进行计算.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
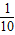 ;
;