题目内容
2010年,我国南方省市遭遇旱涝灾害,为防洪抗旱,某地区大面积植树造林,如图,在区域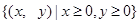 内植树,第一棵树在
内植树,第一棵树在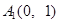 点,第二棵树在
点,第二棵树在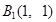 点,第三棵树在
点,第三棵树在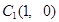 点,第四棵树在
点,第四棵树在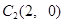 点,接着按图中箭头方向,每隔一个单位种一颗树,那么,第2014棵树所在的点的坐标是( )
点,接着按图中箭头方向,每隔一个单位种一颗树,那么,第2014棵树所在的点的坐标是( )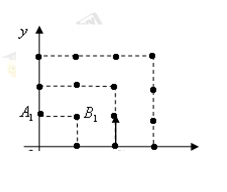
| A.(9,44) | B.(10,44) | C.(10.43) | D.(11,43) |
B
解析试题分析:由题意可得种树的方法是按照一个等差数列3,5,7,…,2n+1排列.由前n项和得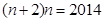 .所以
.所以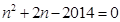 .
.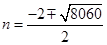 .所以
.所以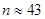 当n=43对应种了1935棵树.由于单数的最后一个落在x轴上.双数的最后一个落在y轴.在坐标为(43,0)向上种44棵即第1979棵的坐标为(44,44).再向左平行移动35格.即第2014棵.及坐标为(10,44)故选B.本题的关键是发现两个规律其一是n为单数时最后一个落在哪个轴上.其二是两个数之间的个数问题.
当n=43对应种了1935棵树.由于单数的最后一个落在x轴上.双数的最后一个落在y轴.在坐标为(43,0)向上种44棵即第1979棵的坐标为(44,44).再向左平行移动35格.即第2014棵.及坐标为(10,44)故选B.本题的关键是发现两个规律其一是n为单数时最后一个落在哪个轴上.其二是两个数之间的个数问题.
考点:1.数列的通项与求和思想.2.两数之间的个数问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在数列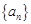 中,若对任意的
中,若对任意的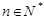 均有
均有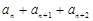 为定值,且
为定值,且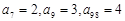 ,则数列
,则数列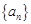 的前100项的和
的前100项的和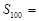 ( )
( )
| A.132 | B.299 | C.68 | D.99 |
数列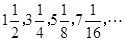 的前
的前 项和
项和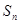 为( ).
为( ).
A.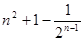 | B.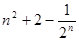 | C.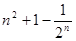 | D.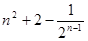 |
若数列 的前
的前 项和
项和 ,则数列
,则数列 的通项公式
的通项公式 ( )
( )
A. | B. | C. | D. |
设数列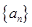 满足
满足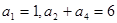 ,且对任意
,且对任意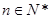 ,函数
,函数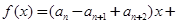
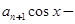
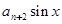 满足
满足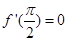 ,若
,若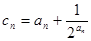 ,则数列
,则数列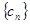 的前
的前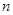 项和
项和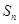 为( )
为( )
A.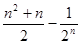 | B.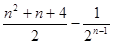 |
C.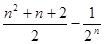 | D. |
若数列 满足
满足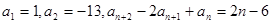 ,则当
,则当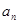 取最小值时
取最小值时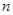 的值为( )
的值为( )
A.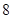 或 或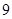 | B.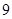 | C.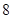 | D. 或 或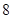 |
已知数列 的首项
的首项 ,且
,且 ,则
,则 为( )
为( )
| A.7 | B.15 | C.30 | D.31 |
已知数列{ }满足
}满足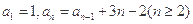 ,则
,则 的通项公式为( )
的通项公式为( )
A.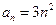 |
B. |
C.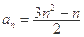 |
D.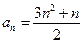 |
已知数列{an}的前n项和Sn满足:Sn+Sm=Sn+m,且a1=1,那么a11=( ).
| A.1 | B.9 | C.10 | D.55 |