题目内容
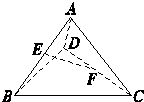
如图所示,在空间四边形ABCD中,点E、F分别是BC、AD上的点,已知AB=4,CD=20,EF=7, ![]() 。求异面直线AB与CD所成的角。
。求异面直线AB与CD所成的角。
120°
解析:
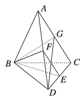
在BD上取一点G,使得![]() ,连结EG、FG
,连结EG、FG
在ΔBCD中,![]() ,故EG//CD,并且
,故EG//CD,并且![]() ,
,
 所以,EG=5;类似地,可证FG//AB,且
所以,EG=5;类似地,可证FG//AB,且![]() ,
,
故FG=3,在ΔEFG中,利用余弦定理可得
cos∠FGE=![]() ,故∠FGE=120°。
,故∠FGE=120°。
另一方面,由前所得EG//CD,FG//AB,所以EG与FG所成的锐角等于AB与CD所成的角,于是AB与CD所成的角等于60°。

练习册系列答案
相关题目
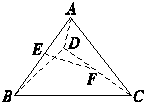 如图所示,在空间四边形ABCD中,E,F分别是AB,CD的中点,请判断向量
如图所示,在空间四边形ABCD中,E,F分别是AB,CD的中点,请判断向量 ,且AD⊥BC,对角线BD=
,且AD⊥BC,对角线BD= ,AC=
,AC= ,求AC和BD所成的角的大小.
,求AC和BD所成的角的大小.