题目内容
(12分)已知f(x)=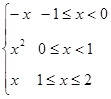
(1)求f(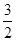 ),f[f(-
),f[f(-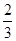 )]值;
)]值;
(2)若f(x)=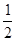 ,求x值;
,求x值;
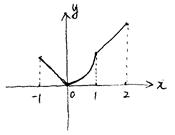
(3)作出该函数简图;
(4)求函数值域.
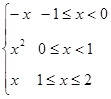
(1)求f(
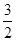 ),f[f(-
),f[f(-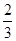 )]值;
)]值;(2)若f(x)=
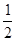 ,求x值;
,求x值;(3)作出该函数简图;
(4)求函数值域.
(1)f[f(-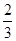 )]=f(
)]=f(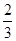 )=
)=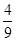 ;(2)x=-
;(2)x=-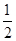 或
或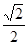
(3)
(4)y∈[0, 2]
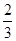 )]=f(
)]=f(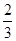 )=
)=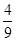 ;(2)x=-
;(2)x=-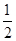 或
或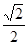
(3)

(4)y∈[0, 2]
判断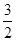 所在范围,选择函数属于那一段,对于f[f(-
所在范围,选择函数属于那一段,对于f[f(-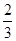 )],先里后外,层层求解。第二问已知函数值求x的值,需要对分段函数讨论;分段函数作图要分段一段一段的作。然后根据图象可以确定函数的值域。
)],先里后外,层层求解。第二问已知函数值求x的值,需要对分段函数讨论;分段函数作图要分段一段一段的作。然后根据图象可以确定函数的值域。
解:(1)f(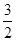 )=
)=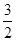 f(-
f(-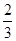 )=
)=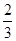
∴f[f(-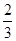 )]=f(
)]=f(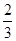 )=
)=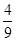
(2)当-1≤x<0时 f(x)=-x=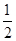
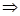 x=-
x=-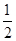 符合题意
符合题意
当0≤x<1时 f(x)=x2=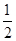
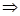 x=
x=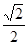 或x=-
或x=-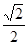 (不合,舍去)
(不合,舍去)
当1≤x≤2时 f(x)=x=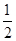 (不合题意,舍去)
(不合题意,舍去)
综上:x=-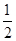 或
或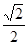
(3)

(4)y∈[0, 2]
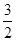 所在范围,选择函数属于那一段,对于f[f(-
所在范围,选择函数属于那一段,对于f[f(-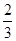 )],先里后外,层层求解。第二问已知函数值求x的值,需要对分段函数讨论;分段函数作图要分段一段一段的作。然后根据图象可以确定函数的值域。
)],先里后外,层层求解。第二问已知函数值求x的值,需要对分段函数讨论;分段函数作图要分段一段一段的作。然后根据图象可以确定函数的值域。解:(1)f(
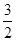 )=
)=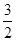 f(-
f(-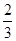 )=
)=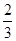
∴f[f(-
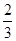 )]=f(
)]=f(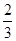 )=
)=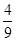
(2)当-1≤x<0时 f(x)=-x=
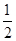
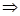 x=-
x=-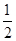 符合题意
符合题意当0≤x<1时 f(x)=x2=
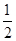
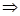 x=
x=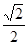 或x=-
或x=-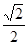 (不合,舍去)
(不合,舍去)当1≤x≤2时 f(x)=x=
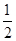 (不合题意,舍去)
(不合题意,舍去)综上:x=-
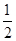 或
或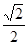
(3)

(4)y∈[0, 2]

练习册系列答案
相关题目
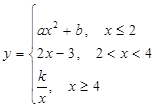 的图象如图所示.
的图象如图所示.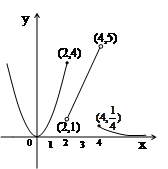
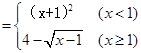 则使得f(x)≥1的自变量x的取值范围为
则使得f(x)≥1的自变量x的取值范围为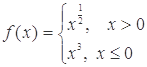 与函数
与函数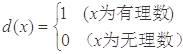 ,则这两个函数图象的公共点的坐标为 .
,则这两个函数图象的公共点的坐标为 .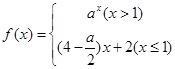 是R上的单调递增函数,则实数a的取值范围为
是R上的单调递增函数,则实数a的取值范围为 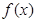
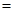
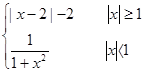 则
则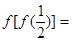 ( )
( )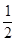
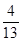

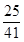

 若
若 ,则实数a = ( )
,则实数a = ( )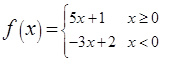 ,求f(1)+f(
,求f(1)+f(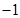 )=_________
)=_________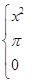
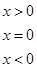 ,则f [ f (-3)]等于
,则f [ f (-3)]等于