题目内容
已知三条不重合的直线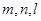 和两个不重合的平面α、β,下列命题中正确命题个数为( )
和两个不重合的平面α、β,下列命题中正确命题个数为( )
①若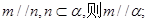
②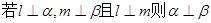
③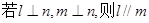
④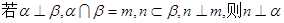
| A.1 | B.2 | C.3 | D.4 |
B
解析试题分析:若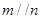 ,
,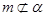 ,则
,则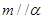 ,所以①错;若
,所以①错;若 在同一平面内,③就正确,否则就不对;②④正确.
在同一平面内,③就正确,否则就不对;②④正确.
考点:1.线面平行的判断定理;2.平面与其法向量的关系;3.面面垂直的性质.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
已知 是三个不同的平面,
是三个不同的平面,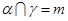 ,
, .则( )
.则( )
A.若 ,则 ,则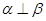 | B.若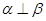 ,则 ,则 |
C.若 ,则 ,则 | D.若 ,则 ,则 |
已知α,β,γ是三个不同的平面,命题“α∥β,且α⊥γ⇒β⊥γ”是真命题,如果把α,β,γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题有 ( )
| A.0个 | B.1个 | C.2个 | D.3个 |
设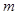 ,
,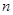 是两条不同直线,
是两条不同直线,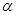 ,
,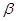 是两个不同平面,则下列命题错误的是( )
是两个不同平面,则下列命题错误的是( )
A.若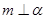 , ,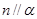 ,则 ,则 | B.若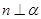 , , ,则 ,则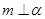 |
C.若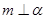 , ,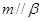 ,则 ,则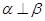 | D.若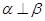 , ,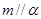 ,则 ,则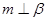 |
已知m,n是两条不同的直线,α,β是两个不同的平面,有下列四个命题:
①若m∥n,n?α,则m∥α;
②若m⊥n,m⊥α,n α,则n∥α;
α,则n∥α;
③若α⊥β,m⊥α,n⊥β,则m⊥n;
④若m,n是异面直线,m?α,n?β,m∥β,则n∥α.
其中正确的命题有( )
| A.①② | B.②③ | C.③④ | D.②④ |
若直线a不平行于平面?,则下列结论成立的是( )
| A.内的所有直线都与直线a异面 |
| B.内不存在与a平行的直线 |
C. 内的直线都与a相交 内的直线都与a相交 |
D.直线a与平面 有公共点 有公共点 |
三棱柱 中,
中,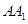 与
与 、
、 所成角均为
所成角均为 ,
, ,且
,且 ,则
,则 与
与 所成角的余弦值为( )
所成角的余弦值为( )
| A.1 | B.-1 | C. | D.- |
对于直线 ,
, 和平面
和平面 ,
, ,使
,使 成立的一个充分条件是( )
成立的一个充分条件是( )
A. , , ∥ ∥ | B. ∥ ∥ , , |
C. , , , , | D. , , , , |
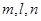 和平面
和平面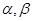 的四个命题:
的四个命题: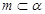 ,
,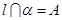 ,点
,点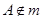 ,则
,则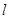 与
与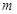 不共面;
不共面;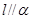 ,
,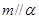 ,且
,且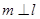 ,
,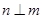 ,则
,则 ;
;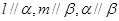 ,则
,则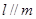 ;
;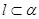 ,
,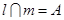 ,
,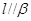 ,
,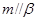 ,则
,则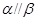 .
.