题目内容
已知在直角坐标系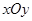 中,曲线
中,曲线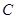 的参数方程为:
的参数方程为: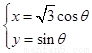 (
(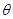 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系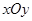 取相同的长度单位,且以原点
取相同的长度单位,且以原点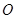 为极点,以
为极点,以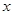 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线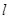 的极坐标方程为:
的极坐标方程为: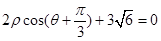 .
.
(Ⅰ)写出曲线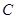 和直线
和直线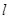 在直角坐标系下的方程;
在直角坐标系下的方程;
(II)设点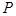 是曲线
是曲线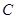 上的一个动点,求它到直线
上的一个动点,求它到直线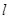 的距离的最小值.
的距离的最小值.
【答案】
(Ⅰ)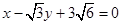 ;(II)
;(II)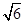 .
.
【解析】
试题分析:(Ⅰ)利用转化公式参数方程、极坐标方程为直角坐标方程;(II)利用点到直线距离公式得点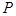 它到直线
它到直线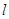 的距离的函数关系式,最后利用函数求最值.
的距离的函数关系式,最后利用函数求最值.
试题解析:(Ⅰ)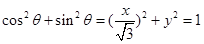 ,
,
所以曲线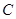 在直角坐标系下的标准方程是
在直角坐标系下的标准方程是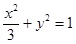
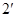
又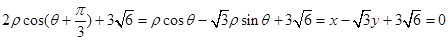
故直线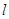 在直角坐标系下的标准方程是
在直角坐标系下的标准方程是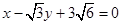
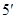
(II)设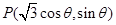 ,于是点
,于是点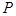 到直线
到直线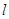 的距离为
的距离为
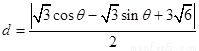
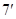
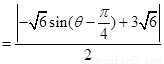
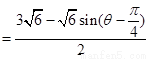
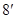
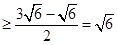
当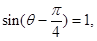 即
即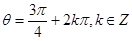 时取等号,此时
时取等号,此时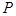 为
为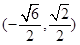
所以点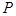 到直线
到直线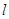 的距离的最小值为
的距离的最小值为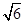
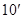
考点:考查选坐标系与参数方程.

练习册系列答案
相关题目
 中,圆锥曲线
中,圆锥曲线 的参数方程为
的参数方程为 (
( 为参数),定点
为参数),定点 ,
, 是圆锥曲线
是圆锥曲线 轴正半轴为极轴建立极坐标系,求经过点
轴正半轴为极轴建立极坐标系,求经过点 且平行于直线
且平行于直线 的直线
的直线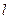 的极坐标方程;
的极坐标方程; 两点,求弦
两点,求弦 的长.
的长. 中,曲线
中,曲线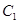 的参数方程为
的参数方程为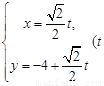 为参数).在极坐标系(与直角坐标取相同的长度单位,且以原点
为参数).在极坐标系(与直角坐标取相同的长度单位,且以原点 为极点,
为极点,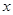 轴的非负半轴为极轴)中,曲线
轴的非负半轴为极轴)中,曲线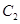 的方程为
的方程为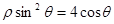 .
. ,求
,求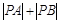 的值.
的值.