Question

设P为双曲线C：

x2

a2

-

y2

b2

=1(a＞0，b＞0)的渐近线在第一象限内的部分上一动点，F为双曲线C的右焦点，A为双曲线C的右准线与x轴的交点，e是双曲线C的离心率，则∠APF的最大值为（　　）

• A、arcsin

  1

  e

• B、arccos

  1

  e

• C、arctan

  1

  e2-1

• D、arccot

  e2-1

Answer 1

分析：根据双曲线的简单性质得：A（

a2

c

，0），F（c，0），P（at，bt） 由直线的斜率公式，得K_PF=

bt

at-c

，K_PA=

bt

at- a 2 c

，再利用根据到角公式，得tan∠APF的表达式，最后利用基本不等式求得tan∠APF的最大值，以及取得取大值时有：cos∠APF=

1

1+(tan∠APF) 2

=

1

e

，结合反三角函数即可表示出∠APF的最大值．

解答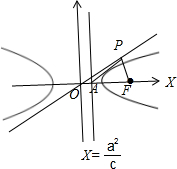：解：由题意得：A（

a2

c

，0），F（c，0），P（at，bt）
由直线的斜率公式，得
K_PF=

bt

at-c

，K_PA=

bt

at- a 2 c

根据到角公式，得
tan∠APF=

bt at-c - bt at- a 2 c

1+ bt at-c  • bt at- a 2 c

化简，得tan∠APF=

b 3

c3t+ a2c t -(a3+ac 2)

≤

b 3

2 c3t• a2c t -(a3+ac 2)

=

b 3

2ac 2- (a3+ac 2)

=

b

a

此时cos∠APF=

1

1+(tan∠APF) 2

=

1

e

则∠APF的最大值为arccos

1

e

故选B

点评：本小题主要考查双曲线的定义、双曲线的简单性质、基本不等式等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．