题目内容
将函数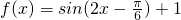 的图象沿向量
的图象沿向量 平移后得到函数g(x)=cos2x的图象,则
平移后得到函数g(x)=cos2x的图象,则 可以是
可以是
- A.
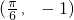
- B.
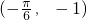
- C.
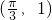
- D.
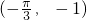
D
分析:可利用函数图象的向量平移公式解决问题,设出平移向量 =(a,b),得向量平移公式
=(a,b),得向量平移公式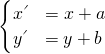 ,代入平移后函数解析式得平移前函数解析式,与已知函数解析式比较即可求得a、b值
,代入平移后函数解析式得平移前函数解析式,与已知函数解析式比较即可求得a、b值
解答:设 =(a,b),函数
=(a,b),函数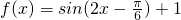 的图象上任意一点(x,y)沿向量
的图象上任意一点(x,y)沿向量 平移后的对应点为(x′,y′)
平移后的对应点为(x′,y′)
则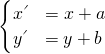 ,
,
∵平移后得到函数g(x)=cos2x的图象,∴(x′,y′)满足函数g(x)=cos2x的解析式,
代入,得y+b=cos[2(x+a)]
化简,得,y=cos[2(x+a)]-b,即y=sin[ +2(x+a)]-b=sin(2x+2a+
+2(x+a)]-b=sin(2x+2a+ )-b
)-b
∴原函数图象上的任意一点满足关系式y=sin(2x+2a+ )-b
)-b
即原函数解析式为y=sin(2x+2a+ )-b
)-b
又∵原函数为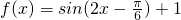
∴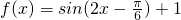 与y=sin(2x+2a+
与y=sin(2x+2a+ )-b为同一个函数.
)-b为同一个函数.
∴2a+ =-
=- +2kπ(k∈Z),-b=1
+2kπ(k∈Z),-b=1
解得,a=- +kπ(k∈Z),b=-1
+kπ(k∈Z),b=-1
∴ 可取
可取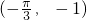
故选 D
点评:本题考查了三角函数的图象变换,函数图象的向量平移公式的运用,简单的三角变换公式的运用
分析:可利用函数图象的向量平移公式解决问题,设出平移向量
 =(a,b),得向量平移公式
=(a,b),得向量平移公式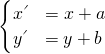 ,代入平移后函数解析式得平移前函数解析式,与已知函数解析式比较即可求得a、b值
,代入平移后函数解析式得平移前函数解析式,与已知函数解析式比较即可求得a、b值解答:设
 =(a,b),函数
=(a,b),函数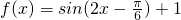 的图象上任意一点(x,y)沿向量
的图象上任意一点(x,y)沿向量 平移后的对应点为(x′,y′)
平移后的对应点为(x′,y′)则
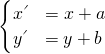 ,
,∵平移后得到函数g(x)=cos2x的图象,∴(x′,y′)满足函数g(x)=cos2x的解析式,
代入,得y+b=cos[2(x+a)]
化简,得,y=cos[2(x+a)]-b,即y=sin[
 +2(x+a)]-b=sin(2x+2a+
+2(x+a)]-b=sin(2x+2a+ )-b
)-b∴原函数图象上的任意一点满足关系式y=sin(2x+2a+
 )-b
)-b即原函数解析式为y=sin(2x+2a+
 )-b
)-b又∵原函数为
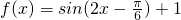
∴
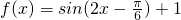 与y=sin(2x+2a+
与y=sin(2x+2a+ )-b为同一个函数.
)-b为同一个函数.∴2a+
 =-
=- +2kπ(k∈Z),-b=1
+2kπ(k∈Z),-b=1解得,a=-
 +kπ(k∈Z),b=-1
+kπ(k∈Z),b=-1∴
 可取
可取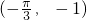
故选 D
点评:本题考查了三角函数的图象变换,函数图象的向量平移公式的运用,简单的三角变换公式的运用

练习册系列答案
相关题目
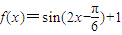 的图象沿向量
的图象沿向量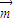 平移后得到函数g(x)=cos2x的图象,则
平移后得到函数g(x)=cos2x的图象,则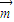 可以是( )
可以是( )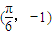
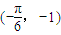
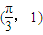
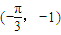
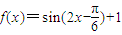 的图象沿向量
的图象沿向量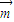 平移后得到函数g(x)=cos2x的图象,则
平移后得到函数g(x)=cos2x的图象,则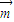 可以是( )
可以是( )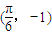
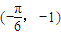
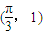
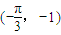
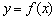 的图象沿向量
的图象沿向量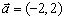 平移后,得到函数
平移后,得到函数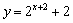 的图象,则函数
的图象,则函数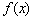 =
.
=
.