题目内容
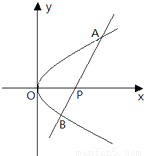
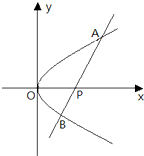 (文)如图,O为坐标原点,过点P(2,0)且斜率为k的直线l交抛物线y2=2x于A(x1,y1),B(x2,y2)两点.
(文)如图,O为坐标原点,过点P(2,0)且斜率为k的直线l交抛物线y2=2x于A(x1,y1),B(x2,y2)两点.
(1)求x1x2与y1y2的值;
(2)求证:OA⊥OB.
解:(1)设直线l的方程为:y=k(x-2)(k≠0),
由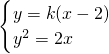 得k2x2-(4k2+2)x+4k2=0,k≠0,△>0,
得k2x2-(4k2+2)x+4k2=0,k≠0,△>0,
则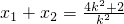 ,x1x2=
,x1x2=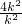 =4,
=4,
y1y2=k2(x1-2)(x2-2)=k2[x1x2-2(x1+x2)+4]=k2•[4-2×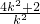 +4]=k2•(-
+4]=k2•(-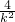 )=-4.
)=-4.
所以x1x2=4,y1y2=-4.
(2)由(1)知,x1x2=4,y1y2=-4,
所以 =(x1,y1)•(x2,y2)=x1x2+y1y2=4-4=0,
=(x1,y1)•(x2,y2)=x1x2+y1y2=4-4=0,
所以 ,即OA⊥OB.
,即OA⊥OB.
分析:(1)设直线l的方程为:y=k(x-2)(k≠0),联立直线方程与抛物线方程构成方程组,消去y后得关于x的二次方程,由韦达定理即可求得x1x2的值,y1y2=k(x1-2)•k(x2-2)=k2[x1x2-2(x1+x2)+4],再代入韦达定理即可求得其值;
(2)要证OA⊥OB,可证明 ,进而转化为证明
,进而转化为证明 =0,借助(1)问的结论容易证明;
=0,借助(1)问的结论容易证明;
点评:本题考查直线与圆锥曲线的位置关系,考查方程思想,韦达定理是解决该类题目常用的基础知识,应准确把握.
由
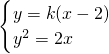 得k2x2-(4k2+2)x+4k2=0,k≠0,△>0,
得k2x2-(4k2+2)x+4k2=0,k≠0,△>0,则
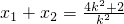 ,x1x2=
,x1x2=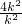 =4,
=4,y1y2=k2(x1-2)(x2-2)=k2[x1x2-2(x1+x2)+4]=k2•[4-2×
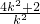 +4]=k2•(-
+4]=k2•(-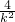 )=-4.
)=-4.所以x1x2=4,y1y2=-4.
(2)由(1)知,x1x2=4,y1y2=-4,
所以
 =(x1,y1)•(x2,y2)=x1x2+y1y2=4-4=0,
=(x1,y1)•(x2,y2)=x1x2+y1y2=4-4=0,所以
 ,即OA⊥OB.
,即OA⊥OB.分析:(1)设直线l的方程为:y=k(x-2)(k≠0),联立直线方程与抛物线方程构成方程组,消去y后得关于x的二次方程,由韦达定理即可求得x1x2的值,y1y2=k(x1-2)•k(x2-2)=k2[x1x2-2(x1+x2)+4],再代入韦达定理即可求得其值;
(2)要证OA⊥OB,可证明
 ,进而转化为证明
,进而转化为证明 =0,借助(1)问的结论容易证明;
=0,借助(1)问的结论容易证明;点评:本题考查直线与圆锥曲线的位置关系,考查方程思想,韦达定理是解决该类题目常用的基础知识,应准确把握.

练习册系列答案
相关题目
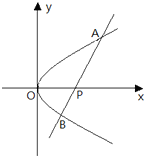 (文)如图,O为坐标原点,过点P(2,0)且斜率为k的直线l交抛物线y2=2x于A(x1,y1),B(x2,y2)两点.
(文)如图,O为坐标原点,过点P(2,0)且斜率为k的直线l交抛物线y2=2x于A(x1,y1),B(x2,y2)两点.
 (II)试证明直线PQ恒过一个定点。
(II)试证明直线PQ恒过一个定点。